题目内容
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为 . 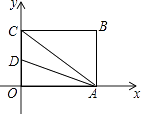
【答案】(0, ![]() )
)
【解析】解:过D作DE⊥AC于E, 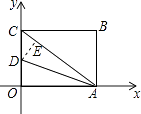
∵四边形ABCO是矩形,B(4,3),
∴OC=AB=3,OA=BC=4,∠CCOA=90°,
∵AD平分∠OAC,
∴OD=DE,
由勾股定理得:OA2=AD2﹣OD2 , AE2=AD2﹣DE2 ,
∴OA=AE=4,
由勾股定理得:AC= ![]() =5,
=5,
在Rt△DEC中,DE2+EC2=CD2 ,
即OD2+(5﹣4)2=(3﹣OD)2 ,
解得:OD= ![]() ,
,
所以D的坐标为(0, ![]() ),
),
故答案为:(0, ![]() ).
).
过D作DE⊥AC于E,根据矩形的性质和B的坐标求出OC=AB=3,OA=BC=4,∠CCOA=90°,求出OD=DE,根据勾股定理求出OA=AE=4,AC=5,在Rt△DEC中,根据勾股定理得出DE2+EC2=CD2 , 求出OD,即可得出答案.本题考查了矩形的性质,角平分线性质,勾股定理的应用,能根据勾股定理得出关于OD的方程是解此题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目