题目内容
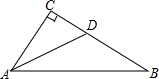 如图,∠ACB=90°,AD是∠CAB的平分线,BC=4,CD=
如图,∠ACB=90°,AD是∠CAB的平分线,BC=4,CD= ,求AC的长.
,求AC的长.
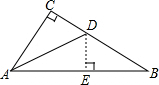 解:
解:过点D作DE⊥AB于E,
在△ADC和△ADE中

∴△ADC≌△ADE(AAS),
∴DE=CD=
 ,AE=AC,
,AE=AC,∴BD=4-
 =
= ,
,在Rt△BDE中,BE=
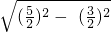 =2,
=2,在Rt△ABC中,设AE=AC=x,
x2+42=(x+2)2,
解得x=3,
∴AC=3.
分析:过点D作DE⊥AB于E,则△ADC≌△ADE,所以DE=CD=
 ,可得BD=
,可得BD= ,在Rt△BDE中,根据勾股定理可得BE=2,再在Rt△ABC中,设AE=AC=x,由勾股定理解得AE的值,即是AC的值.
,在Rt△BDE中,根据勾股定理可得BE=2,再在Rt△ABC中,设AE=AC=x,由勾股定理解得AE的值,即是AC的值.点评:此题主要考查角平分线的性质和勾股定理以及全等三角形的判定和性质,难度中等,作辅助线很关键.

练习册系列答案
相关题目
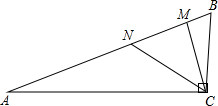 如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是
如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是 10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( )
10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( ) 如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( ) 如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE.
如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE. 如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.
如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.