题目内容
如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
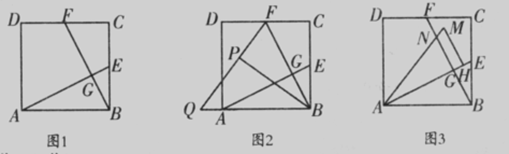
(1)证明:∵E、F分别是正方形ABCD边BC、CD的中点,∴CF=BE,
∵Rt△ABE≌Rt△BCF ∴∠BAE=∠CBF
又∵∠BAE+∠BEA=900,∴∠CBF+∠BEA=900,
∴∠BGE=900, ∴AE⊥BF
(2)根据题意得:FP=FC,∠PFB=∠BFC,∠FPB=900,
∵CD∥AB, ∴∠CFB=∠ABF,∴∠ABF=∠PFB.∴QF=QB
令PF=k(k>O),则PB=2k,
在Rt△BPQ中,设QB=x, ∴x2=(x-k)2+4k2, ∴x= k,
k,
∴sin∠BQP=
由题意得:∠BAE=∠EAM,又AE⊥BF, ∴AN=AB=2,
∵ ∠AHM=900, ∴GN//HM, .
∴ ∴
∴
∴ 四边形GHMN=SΔAHM - SΔAGN=1一 =
= 
所以四边形GHMN的面积是

练习册系列答案
相关题目
 = _ _ ______.
= _ _ ______.  是多项式 B.
是多项式 B. 由三项组成
由三项组成 是3次的多项式 D.
是3次的多项式 D. 的系数是2
的系数是2 .则此人在该市停留期间有且仅有
.则此人在该市停留期间有且仅有 B、
B、 C、
C、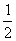 D、
D、


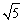 ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为【
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为【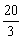 ,
,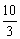 ) B.(
) B.(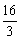 ,
,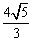 ) C.(
) C.(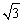 )
)
 ,连接AB,AD,BD,弦AB不经过圆心O.延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB,AD,BD,弦AB不经过圆心O.延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF. 的长;
的长; BD;
BD;
 中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图所示。
中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图所示。
