题目内容
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1). 
(1)在图中标出△ABC外心D的位置,并直接写出它的坐标;
(2)判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由.
【答案】
(1)解:如图,△ABC的外心D点的坐标为(3,2);

(2)解:△ABC的外接圆D与x轴相交,与y轴相离,
理由:∵由题意可知△ABC为直角三角形,AB=2,CB=4,
∴斜边即为外接圆的直径,
半径等于 ![]() AC=
AC= ![]() =
= ![]() .
.
又∵外心坐标为(3,2),
∴外心D到x轴的距离为2,到y轴的距离为3,
∵2< ![]() ,3>
,3> ![]() ,
,
∴△ABC的外接圆D与x轴相交,与y轴相离.
【解析】(1)根据A点的坐标建立平面直角坐标系,找出线段AC的中点即为D点;(2)根据D点坐标即可得出结论.
【考点精析】解答此题的关键在于理解三角形的外接圆与外心的相关知识,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.

【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).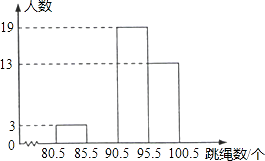
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.



