题目内容
如图,在四边形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F.
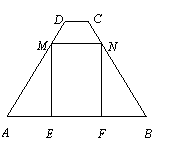 (1)求梯形ABCD的面积;
(1)求梯形ABCD的面积;
(2)设AE=x,用含x的代数式表示四边形MEFN的面积.
(3)试判断四边形MEFN能否为正方形,若能,求出正方
形MEFN的面积;若不能,请说明理由.
(1)分别过D、C两点作DG⊥AB于点G,
CH⊥AB于点H.易证四边形DGHC为矩形,
∴GH=DC=1.又可证△AGD≌△BHC.
∴ AG=BH=3. 在Rt△AGD中,
AG=3,AD=5,∴ DG=4.
∴ .
.
(2)易证四边形MEFN为矩形, △MEA≌△NFB, △MEA∽△DGA
∴ AE=BF. 设AE=x,则EF=7-2x.∴ . ME=
. ME= .
.
∴  .
.
(3)能.四边形MEFN为正方形,则ME=EF. 由(2)知,AE=x,
EF=7-2x,ME= .
.
∴  7-2x.解得
7-2x.解得 .∴ EF=
.∴ EF= <4.
<4.
∴ .
.

练习册系列答案
相关题目
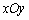 中,定义直线
中,定义直线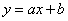 为抛物线
为抛物线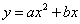 的特征直线,
的特征直线,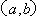 为其特征点.设抛物线
为其特征点.设抛物线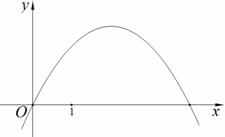
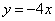 上一点,求点D及点C的坐标;
上一点,求点D及点C的坐标; 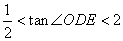 ,则b的取值范围是 .
,则b的取值范围是 . 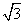 ,则该矩形的两条对角线
,则该矩形的两条对角线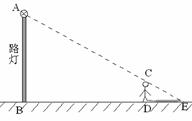
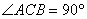 ,BE平分∠ABC,
,BE平分∠ABC,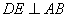 ,
,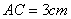 ,那么
,那么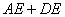 的值为( )
的值为( )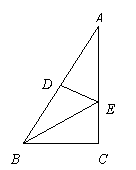
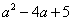 变为 ,从而无论a取何值,
变为 ,从而无论a取何值,