题目内容
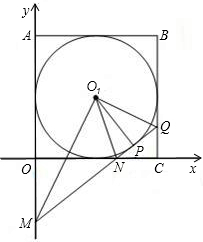
如图，坐标系中，四边形OABC与CDEF都是正方形，OA=2，M、D分别是AB、BC的中点，当把正方形CDEF绕点C旋转某个角度或沿y轴上下平移后，如果点F的对应点为F′，且OF′=OM．则点F′的坐标是________．
（0，
）或（0，-）或（-1，2）或（1，2）．
分析：以O为圆心，OM为半径画圆，交y轴于两点，求得OM的长，可得F′可能的两种情况；以C为圆心CF长为半径做圆C交圆O于两点，可得以点C为圆心，旋转得到的2个点．
解答：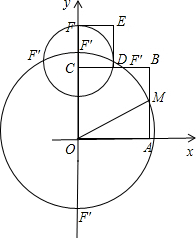
解：①若把正方形CDEF沿轴上下平移，
以O为原点OM长为半径做圆O，OM=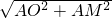
=，
∴在y轴上的2个点的坐标为（0，），（0，-）；
②若把正方形CDEF绕点C旋转某个角度，
以C为圆心CF长为半径做圆C交圆O于两点，此时两点为（-1，2），（1，2）．
故答案为：（0，）或（0，-）或（-1，2）或（1，2）．
点评：本题综合考查了点的平移或旋转问题；利用圆判断出平移或旋转后的点是解决本题的关键．
）或（0，-）或（-1，2）或（1，2）．分析：以O为圆心，OM为半径画圆，交y轴于两点，求得OM的长，可得F′可能的两种情况；以C为圆心CF长为半径做圆C交圆O于两点，可得以点C为圆心，旋转得到的2个点．
解答：
解：①若把正方形CDEF沿轴上下平移，以O为原点OM长为半径做圆O，OM=
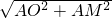=，∴在y轴上的2个点的坐标为（0，
），（0，-）；②若把正方形CDEF绕点C旋转某个角度，
以C为圆心CF长为半径做圆C交圆O于两点，此时两点为（-1，2），（1，2）．
故答案为：（0，
）或（0，-）或（-1，2）或（1，2）．点评：本题综合考查了点的平移或旋转问题；利用圆判断出平移或旋转后的点是解决本题的关键．
练习册系列答案
相关题目
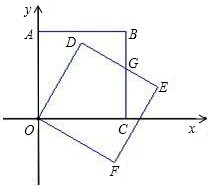在直角坐标系中，正方形OABC的两边OC、OA分别在x轴、y轴上，A点的坐标为（0、4）．
