��Ŀ����
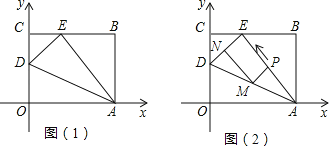
����Ŀ����ͼ��1����OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪ����ԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=5��OC=4����OC����ȡһ��D������ֽƬ��AD��ת��ʹ��O����BC���ϵĵ�E����
��1����ֱ��д��D��E��������ꣻ
��2����ͼ��2�����߶�AE����һ����P������A��E�غϣ����Ե�A��AE�����������˶����˶����ٶ�Ϊÿ��1����λ���ȣ����˶�ʱ��Ϊt�룬����P��ED��ƽ���߽�AD�ڵ�M������M��AEƽ���߽�DE�ڵ�N�����ı���PMNE�����S��ʱ��t֮��ĺ�����ϵʽ��
��3���ڣ�2���������£���tΪ��ֵʱ����A��M��EΪ������������ǵ��������Σ�
���𰸡���1����0��![]() ����2��S����PMNE= -
����2��S����PMNE= -![]() t2+
t2+![]() t��3��t=
t��3��t=![]() ��t=2
��t=2![]() ʱ����A��M��EΪ�����������Ϊ����������
ʱ����A��M��EΪ�����������Ϊ����������
��������
��1���ȸ��ݹ��ɶ������BE�ij��������ɵó�CE�ij������E�����꣬���ù��ɶ��������OD���ɣ�
��2�����жϳ���APM�ס�AED����ʾ��PM�������![]() ȷ������ֵ��
ȷ������ֵ��
��3���������������������AEΪ���������εĵף���ME=MA��������λ�����M�����꣬����������AEΪ���������ε�������AM=AE=5�����ù��ɶ���������������������ɣ�
��1���������֪���ۺ�AD���ı���OAED�ĶԳ��ᣬ
����Rt��ABE��AE=AO=5��AB=4��
BE= ![]() ��
��
��CE=2��
��E��������2��4����
��Rt��DCE��DC2+CE2=DE2��
�֡�DE=OD��
�ࣨ4��OD��2+22=OD2��
��ã�OD= ![]() ��
��
��D��������0��![]() ����
����
��2����PM��ED��
���APM�ס�AED��
��![]() ��
��
��AP=t��ED= ![]() ��AE=5��
��AE=5��
PM= ![]() ��
��![]() =
=![]() ��
��
��PE=5��t��
���ı���PMNEΪ���Σ�
��S����PMNE=PM��PE=![]() ����5��t��=-
����5��t��=-![]() ��
��
��3������������AEΪ���������εĵף���ME=MA����ͼ1��

��Rt��AED��ME=MA��
��PM��AE��
��PΪAE���е㣬
��t=AP=![]() AE=
AE=![]() ��
��
�֡�PM��ED��
��MΪAD���е㣮
����M��MF��OA������ΪF����MF����OAD����λ�ߣ�
��MF=![]() OD=
OD=![]() ��OF=
��OF=![]() OA=
OA=![]() ��
��
�൱t=![]() ʱ����0��
ʱ����0��![]() ��5������AMEΪ���������Σ�
��5������AME����������
����������AEΪ���������ε�������AM=AE=5����ͼ1��
��Rt��AOD��AD=![]() ��
��
����M��MF��OA������ΪF��
��PM��ED��
���APM�ס�AED��
��![]()
��t=AP=![]() ��
��
��PM=![]() t=
t=![]() ��
��
��t=2![]() ʱ����0��2
ʱ����0��2![]() ��5��
��5��
�ۺϣ���������֪��t=![]() ��t=2
��t=2![]() ʱ����A��M��EΪ�����������Ϊ���������Σ�
ʱ����A��M��EΪ�����������Ϊ���������Σ�