Question

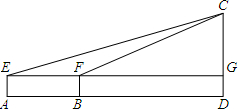马垅中学有一腾飞小广场，广场中间的石雕上有两只海豚，小明一直想知道它的高度，学了第二十八章《解直角三角形》后，他决定去估测这个建筑的高度．他首先站在A处，测得海豚顶部C的仰角∠CEG=21°，然后他往石雕的方向前进10米到达B处，此时测得仰角∠CFG=37°，已知小明的身高1.5米，请你根据以上的数据帮小明算出该石雕CD的高度（参考数据：sin37°≈

3

5

，tan37°≈

3

4

，sin21°≈

9

25

，tan21°≈

3

8

）．

Answer 1

分析：设CG=xm，则由题意可知FG=

4x

3

xm，GE=（

4x

3

+10）m，再利用解直角得出x的值，即可得出CD的长．

解答：解：设CG=xm，
在Rt△CFG中，
∵∠CFG=37°，
∴FG=

CG

tan∠CFG

≈

x

3 4

=

4x

3

∴EG=10+

4x

3

在Rt△CEG中，
∵∠CEG=21°，
∴

CG

EG

=tanE∠CEG
即：

x

4x 3 +10

=

3

8

解得：x=7.5
∴CD=CG+GD=7.5+1.5=9m
∴石雕高9米．

点评：本题考查了解直角三角形的应用，解题的关键是从实际问题中整理出直角三角形模型．