��Ŀ����
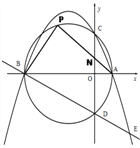
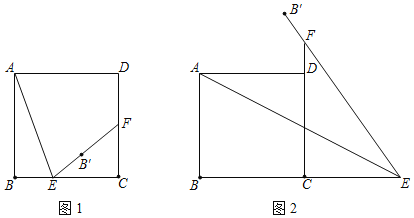
����Ŀ����ͼ����֪������y����![]() x2��bx��c��x���ڵ�A(2��0)��B��һ8��0������y���ڵ�C������A��B��C����ġ�M��y�����һ������ΪD��
x2��bx��c��x���ڵ�A(2��0)��B��һ8��0������y���ڵ�C������A��B��C����ġ�M��y�����һ������ΪD��
(1)��������ߵı���ʽ��Բ��M�����ꣻ
(2)��PΪ��BC������һ�㣨�����B��C�غϣ�������AP��y���ڵ�N�����ʣ�AP��AN�Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
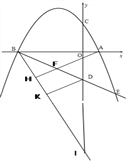
(3)�ӳ��߶�BD���������ڵ�E�����F���߶�BE�ϵ�����һ�㣨�����˵㣩������AF������Q�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶�����F�������߶�FB��ÿ��![]() ����λ���ٶ��˶�����B��ֹͣ���ʵ���F�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����B��ֹͣ���ʵ���F�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
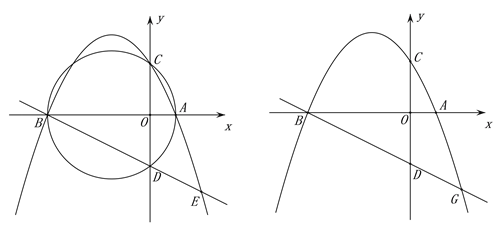
���𰸡���1��M(��3,0) ��2����ֵ��20 ��3��F(��2,��3)
��������(1)�����ݵ�A�͵�B������ó���������ʽ���Ӷ��ó���C�������Լ�AB��AC��BC�ij��ȣ��Ӷ��ó���ABCΪֱ�������Σ�����Բ�����ʵó���M�����ꣻ(2)����������ó���APB�͡�AON���ƣ��Ӷ��ó��𰸣�(3)������B��BE������������BI����y���ڵ�I������A��AH��BI������Ϊ��H,������BE�Ľ��㼴Ϊ�˶�ʱ������ʱ��F��λ��������D��DK��BI������ΪK�����ݹ��ɶ����ó���I�����꣬�Ӷ��ó�BI��AH�ĺ�������ʽ�����ݽ��������г����̵ó���F�����꣮
(1)����A��2��0����B����8��0���������![]() �ã�
�ã�![]() ��
��
��ã�![]() ���������ߵı���ʽΪ��
���������ߵı���ʽΪ��![]() ���� C(0��4)��
���� C(0��4)��
�� BC��4![]() �� AC��2
�� AC��2![]() ��AB��10�� ���ABCΪֱ��������,�ҡ�ACB��90�㣬
��AB��10�� ���ABCΪֱ��������,�ҡ�ACB��90�㣬
�ߡ�ACB��90�㣬 ��ABΪֱ���� ��M(��3��0)��
(2)����ͼ: ��ABΪֱ���� ���APB��90�㣬 �ߡ�APB����AON, ��NAO����BAP��
���APB�ס�AON����![]() �� ��AN��AP��AB��AO��20����Ϊ��ֵ,��ֵ��20��
�� ��AN��AP��AB��AO��20����Ϊ��ֵ,��ֵ��20��
(3)������B��BE������������BI����y���ڵ�I��
����A��AH��BI������Ϊ��H,������BE�Ľ��㼴Ϊ�˶�ʱ������ʱ��F��λ����
����D��DK��BI������ΪK�� ��BEƽ�֡�ABI����DI��DO��4��BO��BK��8��
��DI��x,��KI��2x��8�� ��16��![]() ��
��![]() ��
�� ![]() (��ȥ)��
(��ȥ)��
��I(0��![]() ) �� ��BI����ʽΪ:
) �� ��BI����ʽΪ:![]() �� ��AH����ʽΪ
�� ��AH����ʽΪ![]() ��
��
��BD����ʽΪ![]() �� ��
�� ��![]() �� ������2�� ��F(��2����3) ��
�� ������2�� ��F(��2����3) ��