题目内容
已知边长为4的正方形截去一个角后成为五边形ABCDE（如图），其中AF=2，BF=1．试在AB上求一点P，使矩形PNDM有最大面积．
【答案】分析：要求矩形PNDM的面积，应设DN=x，NP=y，则矩形PNDM的面积为S=xy，再结合已知找出y与x的关系，代入后便可求解．
解答：解：设矩形PNDM的边DN=x，NP=y，
则矩形PNDM的面积S=xy（2≤x≤4），
易知CN=4-x，EM=4-y，
且有
（1分），
即
，
∴y=-
x+5（2分），
S=xy=-
x2+5x（2≤x≤4）（3分），
此二次函数的图象开口向下（4分），
对称轴为x=5（5分）
∴当x≤5时，函数值是随x的增大而增大（6分）
对2≤x≤4来说，
当x=4时，S有最大值（7分）
S最大=-
×42+5×4=12（8分）．
点评：此题综合考查比例线段、二次函数等知识．解决此题的关键在于在AB上找一点P，转变为求PM、PN的值．
解答：解：设矩形PNDM的边DN=x，NP=y，
则矩形PNDM的面积S=xy（2≤x≤4），
易知CN=4-x，EM=4-y，
且有
（1分），即
，∴y=-
x+5（2分），S=xy=-
x2+5x（2≤x≤4）（3分），此二次函数的图象开口向下（4分），
对称轴为x=5（5分）
∴当x≤5时，函数值是随x的增大而增大（6分）
对2≤x≤4来说，
当x=4时，S有最大值（7分）
S最大=-
×42+5×4=12（8分）．点评：此题综合考查比例线段、二次函数等知识．解决此题的关键在于在AB上找一点P，转变为求PM、PN的值．
练习册系列答案
相关题目
CF．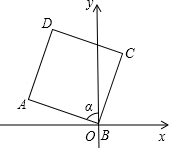
已知边长为1的正方形在坐标系中的位置，如图∠α=75°，求D点的坐标．
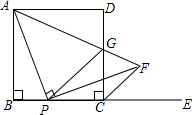如图，已知边长为2的正方形ABCD，P是BC边上一点，E是BC边延长线上一点，过点P作PF⊥AP与∠DCE的平分线CF交于点F．AF与CD交于点G．
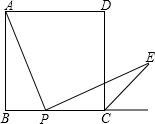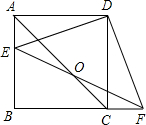
（2013•桂林）如图，已知边长为4的正方形ABCD，P是BC边上一动点（与B、C不重合），连结AP，作PE⊥AP交∠BCD的外角平分线于E．设BP=x，△PCE面积为y，则y与x的函数关系式是（ ）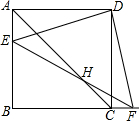
如图，已知边长为4的正方形ABCD，点E在AB上，点F在BC的延长线上，EF与AC交于点H，且AE=CF=m，则四边形EBFD的面积为