题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
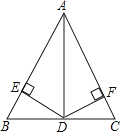
,![]() 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒![]() 过点D作
过点D作![]() 于点F,连接DE、EF.
于点F,连接DE、EF.
![]() 求证:
求证:![]() ;
;
![]() 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
![]() 当t为何值时,
当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.

【答案】(1)证明见解析;(2)能,理由见解析;(3)![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.
【解析】
![]() 在
在![]() 中,
中,![]() ,
,![]() ,根据30°角直角三角形的性质及已知条件即可证得结论;
,根据30°角直角三角形的性质及已知条件即可证得结论;![]() 先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;
先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;![]() 时,四边形EBFD为矩形
时,四边形EBFD为矩形![]() 在Rt△AED中求可得
在Rt△AED中求可得![]() ,由此即可解答;
,由此即可解答;![]() 时,由
时,由![]() 知
知![]() ,则得
,则得![]() ,求得
,求得![]() ,由此列方程求解即可;
,由此列方程求解即可;![]() 时,此种情况不存在.
时,此种情况不存在.
![]() 证明:在
证明:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() 解:能
解:能![]() 理由如下:
理由如下:
![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() 四边形AEFD为平行四边形.
四边形AEFD为平行四边形.
![]() ,
,
![]() .
.
![]() .
.
若使AEFD为菱形,则需![]() ,
,
即![]() ,
,![]() .
.
即当![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
![]() 解:
解:![]() 时,四边形EBFD为矩形.
时,四边形EBFD为矩形.
在![]() 中,
中,![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,由
时,由![]() 四边形AEFD为平行四边形知
四边形AEFD为平行四边形知![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,此种情况不存在.
时,此种情况不存在.
综上所述,当![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】现从A,B两市场向甲、乙两地运送水果,A,B两个水果市场分别有水果35和15吨,其中甲地需要水果20吨,乙地需要水果30吨,从A到甲地运费50元/吨,到乙地30元/吨;从B到甲地运费60元/吨,到乙地45元/吨
(1)设A市场向甲地运送水果x吨,请完成表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A市场 | x |
|
B市场 |
|
|
(2)设总运费为W元,请写出W与x的函数关系式,写明x的取值范围;
(3)怎样调运水果才能使运费最少?运费最少是多少元?