Question

某公司营销两种产品，根据市场调研，发现如下信息：

信息1：销售种产品所获利润(万元)与所售产品(吨)之间存在二次函数关系

.当时， ；当时，．

信息2：销售种产品所获利润 (万元)与所售产品(吨)之间存在正比例函数关系．

根据以上信息，解答下列问题：(1)求二次函数解析式；

(2)该公司准备购进两种产品共10吨，请设计一个营销方案，使销售两种产品获得的利润之和最大，最大利润是多少？

 

Answer 1

【答案】

见解析

【解析】

试题分析：（1）因为当x=1时，y=1.4；当x=3时，y=3.6，代入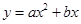

得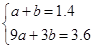 解得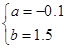 ，所以，二次函数解析式为y=-0.1x²+1.5x；

（2）设购进A产品m吨，购进B产品（10-m）吨，销售A、B两种产品获得的利润之和为W元，根据题意可列函数关系式为：W=-0.1m²+1.5m+0.3（10-m）=-0.1m²+1.2m+3=-0.1（m-6）²+6.6，因为-0.1＜0，根据二次函数的性质知当m=6时，W有最大值6.6，

试题解析：（1）∵当x=1时，y=1.4；当x=3时，y=3.6，

∴ 

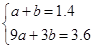
解得 ，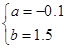

所以，二次函数解析式为y=-0.1x²+1.5x；            3分

（2）设购进A产品m吨，购进B产品（10-m）吨，销售A、B两种产品获得的利润之和为W元，

则W=-0.1m²+1.5m+0.3（10-m）=-0.1m²+1.2m+3=-0.1（m-6）²+6.6，

∵-0.1＜0，

∴当m=6时，W有最大值6.6，

∴购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元．

考点：1.待定系数法求解析式.2.二次函数性质.