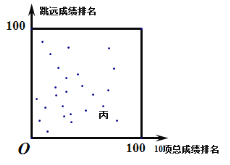
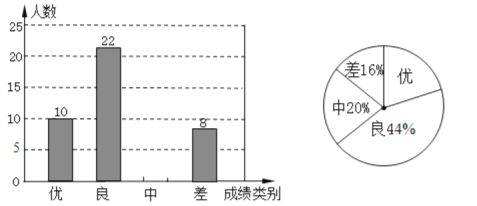
��Ŀ����
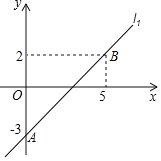
����Ŀ����ͼ��������L1��y����x2��2x��3��x����A��B���㣬��y����M��������L1����ƽ��2����λ�õ�������L2��L2��x����C��D���㣮
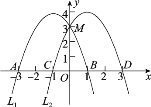
(1)��������L2��Ӧ�ĺ�������ʽ��
(2)������L1��L2��x���Ϸ��IJ����Ƿ���ڵ�N��ʹ��A��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ������N�����ꣻ�������ڣ���˵�����ɣ�
(3)����P��������L1�ϵ�һ������(P�����A��B�غ�)����ô��P����ԭ��ĶԳƵ�Q�Ƿ���������L2�ϣ���˵�����ɣ�
���𰸡���1��y����x2��2x��3����2�����ڣ�N(2��3)��N��(��2��3);��3����Q����������L2�ϣ�
��������
(1)������ƽ�ƣ����������ߵĿ��ڷ���Ϳ��ڴ�С���䣬�����L1��x��Ľ��㣬�����L2��x��Ľ��㣬�������������L2�Ľ���ʽ��
(2)��Ϊ��ƽ�ƣ�����ƽ�Ƶ����ʣ����Ӹ����Ӧ����߶�ƽ������ȣ��ʴ��ڷ��������ĵ�N,�������N�����ꣻ
(3)�����L1�ϵĵ㣨x1��y1����������ù���ԭ��ĶԳƵ㣨-x1��-y1�����ٽ���-x1��-y1�����뺯��L2�Ľ���ʽ����������ͼ���ϣ�����������ͼ���ϣ�
�⣺(1)��y��0���ã�x2��2x��3��0��
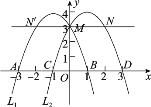
�� ��x1����3��x2��1��
�� ��A(��3��0)��B(1��0) ��
����������L1����ƽ��2����λ��������L2��
�� ��C(��1��0)��D(3��0)��a����1��
�� ��������L2Ϊy����(x��1)(x��3) ��
�� ��y����x2��2x��3��
(2)���ڣ���x��0����y��3��
��M(0��3),
����������L2��L1����ƽ��2����λ�õ��ģ�
�����N(2��3)��L2�ϣ���MN��2��MN��AC��
�֡�AC��2��
��MN��AC��
���ı���ACNMΪƽ���ı��Σ�
ͬ����L1�ϵĵ�N��(��2��3)����N��M��AC��N��M��AC��
�����ı���ACMN����ƽ���ı��Σ�
��N(2��3)��N��(��2��3)������
(3)��P(x1��y1)��L1������һ��(y1��0)��
���P����ԭ��ĶԳƵ�Q(��x1����y1)��
��![]() ��
��
����Q��������L2��
�ã�![]()
���Q����������L2�ϣ�

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�