题目内容
已知:如下图所示,在△ABC中,∠C=90°,BC=5 cm,AC=7 cm.两个动点P、Q分别从B、C两点同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
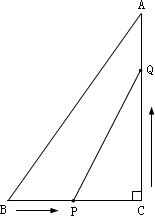
(1)P、Q两点在运动过程中,经过几秒后,△PCQ的面积等于4厘米2?经过几秒后PQ的长度等于5厘米?
(2)在P、Q两点在运动过程中,四边形ABPQ的面积能否等于11厘米2?试说明理由.
答案:
解析:
解析:
|
(1)(ⅰ)设经过x秒后,△PCQ的面积等于4厘米2,此时,PC=5-x,CQ=2x. 由题意,得 解得x1=1,x2=4. 当x=4时,2x=8>7,此时点Q越过A点,不合题意,舍去. 即经过1秒后,△PCQ的面积等于4厘米2. (ⅱ)设经过t秒后PQ的长度等于5厘米.由勾股定理,得(5-t)2+(2t)2=52 整理,得t2-2t=0.解得t1=2,t2=0(不合题意,舍去). 答:经过2秒后PQ的长度等于5厘米. (2)设经过m秒后,四边形ABPQ的面积等于11厘米2.由题意,得 ∵△=(-5)2-4×6.5=-1<0, ∴方程没有实数根.即四边形ABPQ的面积不可能等于11厘米2. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ∠BAF,∠3=∠4=
∠BAF,∠3=∠4= ∠ABE
∠ABE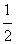 (∠BAF+∠ABE)=
(∠BAF+∠ABE)= ×180°=90°
×180°=90°
