题目内容
已知等边△ABC和等边△A′B′C′的面积分别为4、9,则△ABC、△A′B′C′的边长比为
- A.4:9
- B.16:81
- C.2:3
- D.3:2
C
分析:根据已知条件判断△ABC∽△A′B′C′,然后由相似三角形的面积之比等于相似比的平方来求△ABC、△A′B′C′的边长比.
解答: 解:∵△ABC和△A′B′C′都是等边三角形,
解:∵△ABC和△A′B′C′都是等边三角形,
∴∠ABC=∠A′B′C′=60°,∠BCA=∠B′C′A′=60°,
∴△ABC∽△A′B′C′,
∴ =
=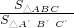 =
= ,
,
∴ =
= ,即△ABC、△A′B′C′的边长比为2:3;
,即△ABC、△A′B′C′的边长比为2:3;
故选C.
点评:本题考查了相似三角形的判定与性质、等边三角形的性质.本题在证明△ABC∽△A′B′C′时,充分利用了等边三角形的性质--等边三角形的三个内角都相等,且都等于60°.
分析:根据已知条件判断△ABC∽△A′B′C′,然后由相似三角形的面积之比等于相似比的平方来求△ABC、△A′B′C′的边长比.
解答:
 解:∵△ABC和△A′B′C′都是等边三角形,
解:∵△ABC和△A′B′C′都是等边三角形,∴∠ABC=∠A′B′C′=60°,∠BCA=∠B′C′A′=60°,
∴△ABC∽△A′B′C′,
∴
 =
=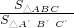 =
= ,
,∴
 =
= ,即△ABC、△A′B′C′的边长比为2:3;
,即△ABC、△A′B′C′的边长比为2:3;故选C.
点评:本题考查了相似三角形的判定与性质、等边三角形的性质.本题在证明△ABC∽△A′B′C′时,充分利用了等边三角形的性质--等边三角形的三个内角都相等,且都等于60°.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

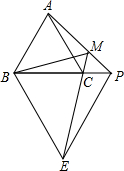 如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM,下列结论:①AP=CE;②∠PME=60°;③BM平分∠AME;④AM+MC=BM,其中正确的有
如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM,下列结论:①AP=CE;②∠PME=60°;③BM平分∠AME;④AM+MC=BM,其中正确的有