题目内容
 如图,⊙O的弦AB与半径OE,OF相交于C、D两点,AC=BD.求证:
如图,⊙O的弦AB与半径OE,OF相交于C、D两点,AC=BD.求证:(1)OC=OD;
(2)
 |
| AE |
 |
| BF |
考点:垂径定理,等腰三角形的判定与性质,圆心角、弧、弦的关系
专题:证明题
分析:(1)连接OA,OB,可以利用SAS判定△OAC≌△OBD,根据全等三角形的对应边相等,可得到OC=OD;
(2)根据(1)中△OAC≌△OBD可得出∠AOC=∠BOO,故可得出结论.
(2)根据(1)中△OAC≌△OBD可得出∠AOC=∠BOO,故可得出结论.
解答: (1)证明:连接OA,OB,
(1)证明:连接OA,OB,
∵AC=BD,
∴∠OAC=∠OBD.
在△OAC与△OBD中,
∵
,
∴△OAE≌△OBF(SAS).
∴OE=OF.
(2)∵由(1)可知,△OAC≌△OBD,
∴∠AOC=∠BOO,
∴
=
.
 (1)证明:连接OA,OB,
(1)证明:连接OA,OB,∵AC=BD,
∴∠OAC=∠OBD.
在△OAC与△OBD中,
∵
|
∴△OAE≌△OBF(SAS).
∴OE=OF.
(2)∵由(1)可知,△OAC≌△OBD,
∴∠AOC=∠BOO,
∴
 |
| AE |
 |
| BF |
点评:本题主要考查了圆的性质,垂径定理,全等三角形的判定等知识的综合应用及推理论证能力.

练习册系列答案
相关题目
已知⊙O的半径是3,点O到直线l的距离为1,则直线l与⊙O的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
在数轴上表示整数的点称为整数点,某数轴的单位长度是1cm,若在这个数轴上随意画出一条长2015cm的线段AB,则被线段AB盖住的整数有( )
| A、2012个或2013个 |
| B、2013个或2014个 |
| C、2014个或2015个 |
| D、2015个或2016个 |
 如图,AB、BC、CD分别与半圆O相切于A、E、D三点,若AB=4,CD=9,求半圆O的半径.
如图,AB、BC、CD分别与半圆O相切于A、E、D三点,若AB=4,CD=9,求半圆O的半径.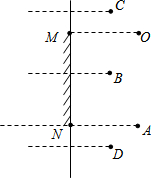 如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有
如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有 如图是3×3正方形网格,其中已有4个小方格涂成了黑色.移动其中一个黑色方块到其他
如图是3×3正方形网格,其中已有4个小方格涂成了黑色.移动其中一个黑色方块到其他