题目内容
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.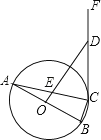
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC= ![]() ,求DE的长.
,求DE的长.
【答案】
(1)
证明:连接OC,
∵OA=OC,
∴∠A=∠OCA,
∵OD⊥AB,
∴∠A+∠AEO=90°,
∵DE=DC,
∴∠DEC=∠DCE,
∵∠AEO=∠DCE,
∴∠AEO=∠DCE,
∴∠OCE+∠DCE=90°,
∴∠OCF=90°,
∴OC⊥CF,
∴CF是⊙O切线.
(2)
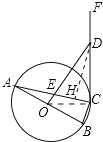
解:作DH⊥AC于H,则∠EDH=∠A,
∵DE=DC,
∴EH=HC= ![]() EC,
EC,
∵⊙O的半径为5,BC= ![]() ,
,
∴AB=10,AC=3 ![]() ,
,
∵△AEO∽△ABC,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴EC=AC﹣AE= ![]() ,
,
∴EH= ![]() EC=
EC= ![]() ,
,
∵∠EDH=∠A,
∴sin∠A=sin∠EDH,
∴ ![]() =
= ![]() ,
,
∴DE= ![]() =
= ![]() =
= ![]()
【解析】(1)连接OC,欲证明CF是⊙O的切线,只要证明∠OCF=90°.
(2)作DH⊥AC于H,由△AEO∽△ABC,得 ![]() =
= ![]() 求出AE,EC,再根据sin∠A=sin∠EDH,得到
求出AE,EC,再根据sin∠A=sin∠EDH,得到 ![]() =
= ![]() ,求出DE即可.本题考查切线的性质、相似三角形的判定和性质、三角函数等知识,解题的关键是添加辅助线,构造相似三角形,属于中考常考题型.
,求出DE即可.本题考查切线的性质、相似三角形的判定和性质、三角函数等知识,解题的关键是添加辅助线,构造相似三角形,属于中考常考题型.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目