题目内容
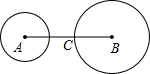 如图,⊙A和⊙B的半径分别为2和3,AB=7,若将⊙A绕点C逆时针方向旋转,当⊙A与⊙B第一次外切时,旋转的角度为
如图,⊙A和⊙B的半径分别为2和3,AB=7,若将⊙A绕点C逆时针方向旋转,当⊙A与⊙B第一次外切时,旋转的角度为
- A.45°
- B.60°
- C.90°
- D.120°
C
分析:根据已知条件画出图形,分别求出BC、A′C、A′B的长,再根据勾股定理得出∠A′CB=90°,即可求出旋转的角度;
解答: 解:∵⊙A和⊙B的半径分别为2和3,AB=7,
解:∵⊙A和⊙B的半径分别为2和3,AB=7,
∴AC=AB-BC=7-3=4,
∵将⊙A绕点C逆时针方向旋转,当⊙A与⊙B第一次外切时,
∴A′B=A′D+BD=2+3=5,
∵A′C=AC=4,BC=3,
∴A′C2+BC2=A′B2,
∴∠A′CB=90°,
∴旋转的角度为90°.
故选C.
点评:此题考查了旋转的性质;解题的关键是根据三角形的三边长度求出角的度数.
分析:根据已知条件画出图形,分别求出BC、A′C、A′B的长,再根据勾股定理得出∠A′CB=90°,即可求出旋转的角度;
解答:
 解:∵⊙A和⊙B的半径分别为2和3,AB=7,
解:∵⊙A和⊙B的半径分别为2和3,AB=7,∴AC=AB-BC=7-3=4,
∵将⊙A绕点C逆时针方向旋转,当⊙A与⊙B第一次外切时,
∴A′B=A′D+BD=2+3=5,
∵A′C=AC=4,BC=3,
∴A′C2+BC2=A′B2,
∴∠A′CB=90°,
∴旋转的角度为90°.
故选C.
点评:此题考查了旋转的性质;解题的关键是根据三角形的三边长度求出角的度数.

练习册系列答案
相关题目
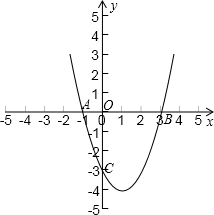 于A、B两点(如图),点C的坐标为(0,-3),且BO=CO
于A、B两点(如图),点C的坐标为(0,-3),且BO=CO
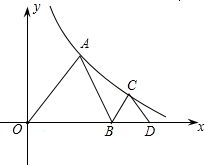 如图,△AOB和△BCD都是等边三角形,点A、C在函数
如图,△AOB和△BCD都是等边三角形,点A、C在函数 于C、D两点且CD=4,抛物线y=ax2+bx+c经过A、B、C三点,顶点为N﹒
于C、D两点且CD=4,抛物线y=ax2+bx+c经过A、B、C三点,顶点为N﹒