题目内容
【问题】如图,在正方形ABCD内有一点P,PA= ,PB=
,PB= ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
【类比研究】如图,若在正六边形ABCDEF内有一点P,且PA= ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ;(2)直接写出正六边形ABCDEF的边长为 .
 ,PB=
,PB= ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
【类比研究】如图,若在正六边形ABCDEF内有一点P,且PA=
 ,PB=4,PC=2.
,PB=4,PC=2.(1)∠BPC的度数为 ;(2)直接写出正六边形ABCDEF的边长为 .

【问题】90°;【类比研究】(1)120°;(2)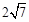
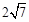
试题分析:【问题】根据旋转的性质得到∠P′BP=90°,BP′=BP=
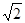 ,P′A=PC=1,∠BP′A=∠BPC,则△BPP′为等腰直角三角形,根据等腰直角三角形的性质得PP′=
,P′A=PC=1,∠BP′A=∠BPC,则△BPP′为等腰直角三角形,根据等腰直角三角形的性质得PP′=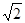 PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,则∠BPC=∠BP′A=45°+90°=135°;
PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,则∠BPC=∠BP′A=45°+90°=135°;【类比研究】把△BPC绕点B逆时针旋转120°,得到了△BP′A,根据旋转的性质得到∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,则∠BP′P=∠BPP′=30°,得到P′H=PH,利用含30°的直角三角形三边的关系得到BH=
 BP′=2,P′H=
BP′=2,P′H=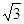 BH=2
BH=2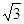 ,得到P′P=2P′H=4
,得到P′P=2P′H=4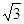 ,再利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;过A作AG⊥BP′于G点,利用含30°的直角三角形三边的关系得到GP′=
,再利用勾股定理的逆定理可得到△APP′为直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;过A作AG⊥BP′于G点,利用含30°的直角三角形三边的关系得到GP′= AP′=1,AG=
AP′=1,AG=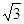 GP′=
GP′=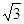 ,然后在Rt△AGB中利用勾股定理即可计算出AB长.
,然后在Rt△AGB中利用勾股定理即可计算出AB长.【问题】得到如图所示的图形,
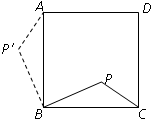
根据旋转的性质可得PB="P′B," PC=P′A
又因为BC="AB," ∴△PBC≌△P′BA,
∴∠PBC="∠P′BA" ,∠BPC="∠BP′A" , PB= P′B=
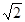 ,
,∴∠P′BP=90°,所以△P′BP为等腰直角三角形,
则有P′P=2,∠BP′P=45°.
又因为PC=P′A=1,P′P =2,PA=
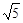 ,
,满足P′A2+ P′P2= PA2,由勾股定理的逆定理可知∠AP′P=90°,
因此∠BPC=∠BP′A=45°+90°=135°.
【类比研究】(1)如图
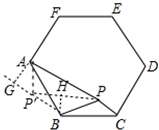
∵六边形ABCDEF为正六边形,
∴∠ABC=120°,
把△BPC绕点B逆时针旋转120°,得到了△BP′A,
∴∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,
∴∠BP′P=∠BPP′=30°,
过B作BH⊥PP′于H,
∵BP′=BP,
∴P′H=PH,
在Rt△BP′H中,∠BP′H=30°,BP′=4,
∴BH=
 BP′=2,P′H=
BP′=2,P′H=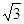 BH=2
BH=2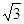 ,
,∴P′P=2P′H=4
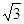 ,
,在△APP′中,AP=2
 ,PP′=4
,PP′=4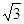 ,AP′=2,
,AP′=2,∵(2
 )2=(4
)2=(4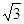 )2+22,
)2+22,∴AP2=PP′2+AP′2,
∴△APP′为直角三角形,且∠AP′P=90°,
∴∠BP′A=30°+90°=120°,
∴∠BPC=120°,
(2)过A作AG⊥BP′于G点,
∴∠AP′G=60°,
在Rt△AGP′中,AP′=2,∠GAP′=30°,
∴GP′=
 AP′=1,AG=
AP′=1,AG=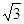 GP′=
GP′=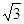 ,
,在Rt△AGB中,GB=GP′+P′B=1+4=5,
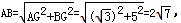
即正六边形ABCDEF的边长为
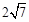 .
.点评:解题的关键是熟练掌握旋转的性质:旋转前后两图形全等,即对应角相等,对应线段相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

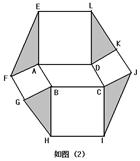

 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12




 cm
cm .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△APD+S△APB=
;③EB⊥ED;④S△APD+S△APB= .其中正确结论的序号是
.其中正确结论的序号是