题目内容
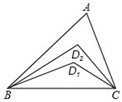
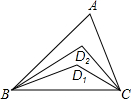 在如图△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,若∠ABD5与∠ACD5的角平分线交D6,则∠BD6C的度数
在如图△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,若∠ABD5与∠ACD5的角平分线交D6,则∠BD6C的度数54°
54°
.分析:根据角平分线的性质可得到:∠ABD1=∠CBD1=
∠ABC,∠ACD1=∠BCD1=
∠ACB,再根据三角形的内角和定理可得:∠BD1C的度数,再根据∠ABD1与∠ACD1的角平分线交于点D2,可得∠D2BC=
∠ABC,∠D2CB=
∠ACB,进而求出∠BD2C=180°-
(∠ABC+∠ACB),以此类推可得到:∠BD6C=180°-
(∠ABC+∠ACB),再次利用三角形内角和代入∠ABC+∠ACB=180°-∠A,即可求出答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 63 |
| 64 |
解答:解:∵∠A=52°,
∴∠ABC+∠ACB=180°-52°=128°,
∵∠ABC与∠ACB的角平分线交于D1,
∴∠ABD1=∠CBD1=
∠ABC,∠ACD1=∠BCD1=
∠ACB,
∴∠CBD1+∠BCD1=
(∠ABC+∠ACB)=
×128°=64°,
∴∠BD1C=180°-
(∠ABC+∠ACB)=180°-64°=116°,
∵∠ABD1与∠ACD1的角平分线交于点D2,
∴∠D2BC=
∠ABC,∠D2CB=
∠ACB,
∴∠D2BC+∠D2CB=
(∠ACB+∠ABC),
∴∠BD2C=180°-
(∠ABC+∠ACB)=180°-
(180°-∠A)=180°-96°=84°,
依此类推,∠BD6C=180°-
(∠ABC+∠ACB)=180°-
(180°-∠A)=180°-126°=54°.
故答案为:54°.
∴∠ABC+∠ACB=180°-52°=128°,
∵∠ABC与∠ACB的角平分线交于D1,

∴∠ABD1=∠CBD1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBD1+∠BCD1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BD1C=180°-
| 1 |
| 2 |
∵∠ABD1与∠ACD1的角平分线交于点D2,
∴∠D2BC=
| 3 |
| 4 |
| 3 |
| 4 |
∴∠D2BC+∠D2CB=
| 3 |
| 4 |
∴∠BD2C=180°-
| 3 |
| 4 |
| 3 |
| 4 |
依此类推,∠BD6C=180°-
| 63 |
| 64 |
| 63 |
| 64 |
故答案为:54°.
点评:此题主要考查角平分线的性质和三角形的内角和定理,关键是根据三角形的角平分线的性质求出∠ABC+∠ACB与∠A的关系,并能找出∠BDnC与∠A的关系规律.

练习册系列答案
相关题目
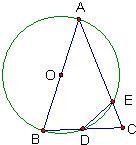 10、如图△ABC中,AB=AC,以AB为直径的⊙O交BC,AC分别为在D,E.则下列判断:①BD=CD;②BD=DE;③AE=DE;④△ABC为锐角三角形.其中正确的判断有( )
10、如图△ABC中,AB=AC,以AB为直径的⊙O交BC,AC分别为在D,E.则下列判断:①BD=CD;②BD=DE;③AE=DE;④△ABC为锐角三角形.其中正确的判断有( ) 如图△ABC中,点D、E分别在AC、AB上,AE=3,EB=5,AD=4,DC=2,则
如图△ABC中,点D、E分别在AC、AB上,AE=3,EB=5,AD=4,DC=2,则 在如图△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,若∠ABD5与∠ACD5的角平分线交D6,则∠BD6C的度数________.
在如图△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,若∠ABD5与∠ACD5的角平分线交D6,则∠BD6C的度数________.