题目内容
如图,在Rt△ABC中,∠ACB=90º,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.
 |
在Rt△ABC中,∠ACB=90º,AC=3cm,BC=4cm.∴AB=5 cm. )
由运动可知,BP=t,且△PBC为等腰三角形有三种可能:
若BP=PC,则∠B=∠PCB.∵∠ACB=90°,∴∠PAC=∠PCA,
∴PC=PA,∴t=BP= AB=
AB= .
.
若BP=BC,则t=4.
若BC=PC,过点C作CH⊥AB,则BP=2BH.由CH×AB=BC×AC,得CH= .
.
在Rt△BHC中,由勾股定理得BH= .
.
∴t=BP= .
.
综上所述,符合要求的t的值有3个,分别是  ,4,
,4, (秒).
(秒).

练习册系列答案
相关题目
 图的概率是( )
图的概率是( )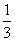 B.
B.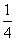 C.
C.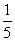 D.
D.
 的度数;
的度数;
 的图像上,则a的值为 .
的图像上,则a的值为 . +
+ -
- ;
;  的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( ) C、5或
C、5或
 的相反数是 .
的相反数是 .