题目内容
 (2012•泰州一模)如图,A(-2,1)、B(-1,m)为反比例函数y=
(2012•泰州一模)如图,A(-2,1)、B(-1,m)为反比例函数y=| k | x |
(1)求k的值及直线AB的解析式;
(2)若点P为x轴上一点,且满足△OAP的面积为3,求出P点坐标.
分析:(1)将A的坐标代入反比例解析式中求出k的值,确定出反比例函数解析式,将B的坐标代入反比例解析式中,得到关于m的方程,求出方程的解得到m的值,确定出B的坐标,设直线AB的解析式为y=kx+b(k≠0),将Ah和B的坐标代入,得到关于k与b的方程组,求出方程组的解得到k与b的值,确定出直线AB的解析式;
(2)设P坐标为(x,0),可得出OP=|x|,A的纵坐标即为三角形AOP中,OP边上的高,利用三角形的面积公式及已知的面积列出关于x的方程,求出方程的解得到x的值,即可确定出P的坐标.
(2)设P坐标为(x,0),可得出OP=|x|,A的纵坐标即为三角形AOP中,OP边上的高,利用三角形的面积公式及已知的面积列出关于x的方程,求出方程的解得到x的值,即可确定出P的坐标.
解答:解:(1)将A(-2,1)代入反比例解析式得:1=
,
解得:k=-2,
∴反比例解析式为y=-
,
将B(-1,m)代入反比例解析式得:m=-
=2,
∴B(-1,2),
设直线AB解析式为y=kx+b(k≠0),
将A和B坐标代入得:
,
解得:
,
∴一次函数解析式为y=x+3;
(2)设P(x,0),则OP=|x|,
∴S△AOP=
×1×|x|=3,即|x|=6,
解得:x=6或x=-6,
则P坐标为(6,0)或(-6,0).
| k |
| -2 |
解得:k=-2,
∴反比例解析式为y=-
| 2 |
| x |
将B(-1,m)代入反比例解析式得:m=-
| 2 |
| -1 |
∴B(-1,2),
设直线AB解析式为y=kx+b(k≠0),
将A和B坐标代入得:
|
解得:
|
∴一次函数解析式为y=x+3;
(2)设P(x,0),则OP=|x|,
∴S△AOP=
| 1 |
| 2 |
解得:x=6或x=-6,
则P坐标为(6,0)或(-6,0).
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
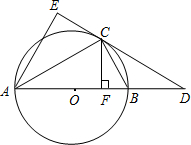 (2012•泰州一模)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(2012•泰州一模)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.