题目内容
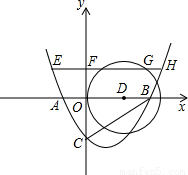
(2001•武汉)如图,关于x的二次函数y=x2-2mx-m的图象与x轴交于A(x1,0)、B(x2,0)两点(x2>0>x1),与y轴交于C点,且∠BAC=∠BCO.(1)求这个二次函数的解析式;
(2)以点D(
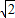 ,0)为圆心作⊙D,与y轴相切于点O.过抛物线上一点E(x3,t)(t>0,x3<0)作x轴的平行线与⊙D交于F、G两点,与抛物线交于另一点H.问:是否存在实数t,使得EF+GH=FG?如果存在,求出t的值;如果不存在,请说明理由.
,0)为圆心作⊙D,与y轴相切于点O.过抛物线上一点E(x3,t)(t>0,x3<0)作x轴的平行线与⊙D交于F、G两点,与抛物线交于另一点H.问:是否存在实数t,使得EF+GH=FG?如果存在,求出t的值;如果不存在,请说明理由.
【答案】分析:(1)中求函数解析式即要求m的大小,由图可知,OC=|m|,又抛物线与x轴交于A、B两点,则OA•OB=m,且m>0,根据题设条件可推得△BCO∽△CAO,帮CO2=OA•OB即m2=m,从而求出m=1(m=0不合题意,舍去).
(2)是一道存在型探索问题,可先假设符合题意的t值存在,再把EF+GH=FG作为已知条件结合题设与相关知识进行演算推证,若求出合适的t的值,则假设成立;若求不出t值或所求值与已知矛盾,则假设不成立.
解答:解:(1)∵∠BAC=∠BCO,∠BOC=∠COA=90°
∵△BCO∽△CAO,
∴ ,
,
∴CO2=AO•OB.
由已知可得:AO=|x1|=-x1,OB=|x2|=x2
∵x1x2=-m<0,
∴m>0,
∴CO=m,AO•BO=m
∴m2=m,m=1,m=0(舍去),
∴抛物线的解析式为:y=x2-2x-1;

(2)存在实数t,使得EF+GH=FG.
过D作DM⊥EH于M,连接DG,
∵EH∥x轴,E(x3,t),
∴DM=t,
∵DG=DO=
∴FG=2MG=2 =2
=2 ,
,
由EF+GH=FG得EH=2FG;
又∵EH∥x轴,E(x3,t),
∴设H(x4,t)
∵E、H是抛物线上的两点,
∴x32-2x3-1=t,x42-2x4-1=t,
即x3、x4是方程的两个不相等的根,
∴x3+x4=2,x3•x4=-(1+t),
∵x3<0
∴x4>0
∴EH=x4-x3= =
= =2
=2 ,
,
∴2 =4
=4 ,
,
即4t2+t-6=0,
解这个方程得t1= ,t2=-
,t2=- (舍去),
(舍去),
故存在实数t= ,使得EF+GH=FG.
,使得EF+GH=FG.
点评:本题是函数与圆的综合题,考查了相似三角形、韦达定理等知识,综合性较强.
(2)是一道存在型探索问题,可先假设符合题意的t值存在,再把EF+GH=FG作为已知条件结合题设与相关知识进行演算推证,若求出合适的t的值,则假设成立;若求不出t值或所求值与已知矛盾,则假设不成立.
解答:解:(1)∵∠BAC=∠BCO,∠BOC=∠COA=90°
∵△BCO∽△CAO,
∴
 ,
,∴CO2=AO•OB.
由已知可得:AO=|x1|=-x1,OB=|x2|=x2
∵x1x2=-m<0,
∴m>0,
∴CO=m,AO•BO=m
∴m2=m,m=1,m=0(舍去),
∴抛物线的解析式为:y=x2-2x-1;

(2)存在实数t,使得EF+GH=FG.
过D作DM⊥EH于M,连接DG,
∵EH∥x轴,E(x3,t),
∴DM=t,
∵DG=DO=

∴FG=2MG=2
 =2
=2 ,
,由EF+GH=FG得EH=2FG;
又∵EH∥x轴,E(x3,t),
∴设H(x4,t)
∵E、H是抛物线上的两点,
∴x32-2x3-1=t,x42-2x4-1=t,
即x3、x4是方程的两个不相等的根,
∴x3+x4=2,x3•x4=-(1+t),
∵x3<0
∴x4>0
∴EH=x4-x3=
 =
= =2
=2 ,
,∴2
 =4
=4 ,
,即4t2+t-6=0,
解这个方程得t1=
 ,t2=-
,t2=- (舍去),
(舍去),故存在实数t=
 ,使得EF+GH=FG.
,使得EF+GH=FG.点评:本题是函数与圆的综合题,考查了相似三角形、韦达定理等知识,综合性较强.

练习册系列答案
相关题目
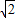 ,0)为圆心作⊙D,与y轴相切于点O.过抛物线上一点E(x3,t)(t>0,x3<0)作x轴的平行线与⊙D交于F、G两点,与抛物线交于另一点H.问:是否存在实数t,使得EF+GH=FG?如果存在,求出t的值;如果不存在,请说明理由.
,0)为圆心作⊙D,与y轴相切于点O.过抛物线上一点E(x3,t)(t>0,x3<0)作x轴的平行线与⊙D交于F、G两点,与抛物线交于另一点H.问:是否存在实数t,使得EF+GH=FG?如果存在,求出t的值;如果不存在,请说明理由.