题目内容
如图,在△ 中,
中, ,
, ,点
,点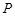 是△
是△ 内一点,且
内一点,且 .
.

(1)求证:△ ∽△
∽△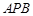 ;
;
(2)试求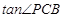 的值.
的值.
 中,
中, ,
, ,点
,点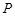 是△
是△ 内一点,且
内一点,且 .
.
(1)求证:△
 ∽△
∽△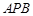 ;
;(2)试求
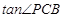 的值.
的值.(1)证明见解析;(2)2.
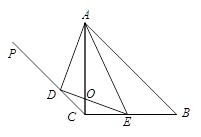
试题分析:(1)应用△ABC中角的关系求出∠PAC=∠PBA和∠APB=∠APC即可证得;(2)由等腰直角三角形,相似三角形的性质和锐角三角函数定义即可求得.
试题解析:
(1)∵在△ABC中,∠ACB=90º,AC=BC
∴∠BAC=45º,即∠PAC+∠PAB=45º,
又在△APB中,∠APB=135º,
∴∠PBA+∠PAB=45º,
∴∠PAC=∠PBA,
又∠APB=∠APC,
∴△CPA∽△APB.
(2)∵△ABC是等腰直角三角形,
∴
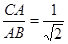 ,
,又∵△CPA∽△APB,
∴
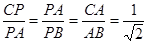 ,
,令CP=k,则PA=
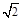 k,PB=2k,
k,PB=2k,又在△BCP中,∠BPC=360º-∠APC-∠BPC=90º,
∴
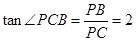

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
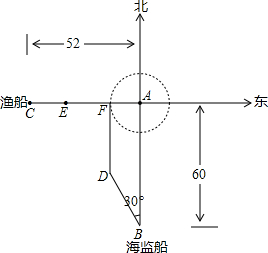
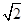 ≈1.4,
≈1.4,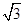 ≈1.7)
≈1.7)
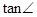 BAE = y,求y关于x的函数解析式,并写出它的定义域;
BAE = y,求y关于x的函数解析式,并写出它的定义域;



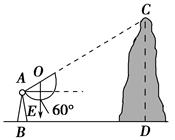
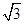 +1.6)m B.(12
+1.6)m B.(12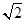 +1.6)m D.4
+1.6)m D.4 ;
; ;
; ;
; .
. 中,
中, ,
, ,
,  是
是 上一点.若
上一点.若 ,那么
,那么 的长为( )
的长为( )


 ;
;
 +
+
 .
.