Question

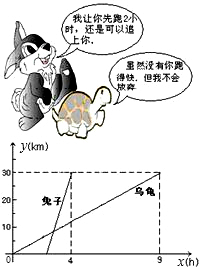龟兔赛跑中，由于兔子途中睡大觉结果输给了乌龟，事后兔子认真总结教训又约乌龟进行了一次比赛，二者从森林甲地出发到森林乙地，赛跑过程中路程随时间变化的图象如图所示
（1）甲地到乙地的路程多长？二者的速度分别是多少？
（2）分别求出表示龟和兔赛跑过程的函数关系式；
（3）免子出发多长时间赶上乌龟？此时它们跑过了多远？

Answer 1

分析：（1）由图可得路程及龟兔的速度；
（2）根据一次函数的标准式．然后代入图中整点的数据，即可得龟和兔赛跑过程的函数关系式；
（3）由第二问的关系式，此问题即转化为求方程组的解问题．

解答：解：（1）甲地到乙地的路程是30km
龟9小时跑了30km，速度=30÷9=3

1

3

（km/h）
兔4-2=2小时跑了30km，速度30÷2=15km/h（3分）

（2）设龟赛跑过程的函数关系式为y=k₁x，把x=9，y=30代入得
9k₁=30解得k₁=

10

3

答：龟赛跑过程的函数关系式是y=

10

3

x．（5分）
设兔赛跑过程的函数关系式为y=k₂x+b
把x=2，y=0；x=4，y=30别代入得

2k2+b=0 4k2+b=30

解得

k2=15 b=-30

答：兔在赛跑过程的函数关系式是y=15x-30．（7分）

（3）解方程组

y= 10 3 x y=15x-30

得

x=2 4 7 y=8 4 7

（9分）
答：兔子出发2

4

7

-2=

4

7

小时赶上乌龟，此时它们跑了8

4

7

km．（10分）

点评：根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．本题还考查了学生的阅读理解及读图能力．