题目内容
已知抛物线
经过原点.与
轴相交于另一点N，直线
与坐标轴分别交于A、D两点，与抛物线相交于点B(1，m)、C(2，2)两点．
(1)求直线与抛物线的解析式；
(2)若(1)中抛物线在轴上方的部分有一动点P(，
)，设
，当
为何值时，△PON的面积有最大值?
(3)若P点保持(2)中的运动路线，是否存在△PON，使其面积等于△OCN面积的
?若存在，求出点P的位置；若不存在，请说明理由．
解：(1)将点c(2，2)代人y=kx+4得 2k+4=2
∴k=－1
∴直线的解析式为
∵当x=l时，y=3 ∴B点坐标为(1,3)
将B(1,3)、C(2，2)、O(0，0)代入
得
∴抛物线的解折式为
(2)∵ON长度一定
∴当P点到
轴的距离最大时，△PON的面积有最大值，这时P是抛物线的顶点，坐标为
，这时
(3)存在．在抛物线上 当
时，
解之得
∴
∴
设P点坐标为
根据题意得
∴
把代入得：
解之得
∴P点坐标为
练习册系列答案
阅读快车系列答案
相关题目
如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1经过抛物线上一点B（-2，m），且与y轴、直线x=2分别交于点D、E．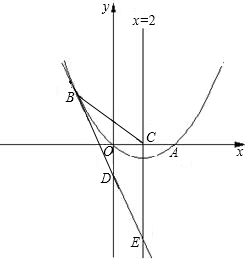
（1）求m的值与抛物线的解析式．
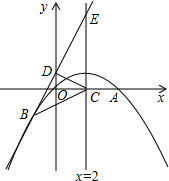+1经过抛物线上一点B（m，-3），且与y轴、直线x=2分别交于点D，E．
如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1经过抛物线上一点B（-2，m），且与y轴、直线x=2分别交于点D、E，