Question

【题目】如图所示，于点于点交于点且平分．

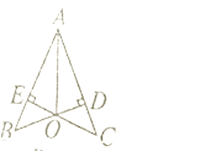
图中有多少对全等三角形？请一一列举出来(不必说明理由)；

求证:

Answer 1

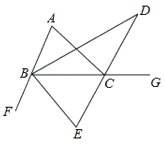
【答案】（1）图中有4对全等三角形，分别是：△AEO≌△ADO，△ADB≌△AEC，△ABO≌△ACO，△EOB≌△DOC；（2）见解析.

【解析】

（1）直接利用AAS证明△AEO≌△ADO，得到AE＝AD，然后利用ASA证明△ADB≌△AEC，得到AB＝AC，再利用SAS证明△ABO≌△ACO，得到∠B＝∠C，BO＝CO，最后利用ASA证明△EOB≌△DOC即可知共有4对全等三角形；

（2）根据全等三角形的性质可直接得出结论.

解：（1）图中有4对全等三角形，分别是：△AEO≌△ADO，△ADB≌△AEC，△ABO≌△ACO，△EOB≌△DOC；

证明：∵AO平分∠BAC，

∴∠EAO＝∠DAO，

∵CE⊥AB，BD⊥AC，

∴∠AEO＝∠ADO＝90°，

∴在△AEO和△ADO中，，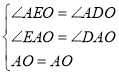

∴△AEO≌△ADO（AAS），

∴AE＝AD，

在△ADB和△AEC中，，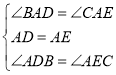

∴△ADB≌△AEC（ASA），

∴AB＝AC，

在△ABO和△ACO中，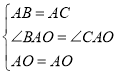

∴△ABO≌△ACO（SAS），

∴∠B＝∠C，BO＝CO，

在△EOB和△DOC中，，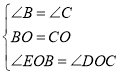

∴△EOB≌△DOC（ASA）；

（2）由（1）可得：△EOB≌△DOC，

∴BE＝CD．