Question

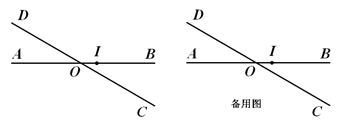
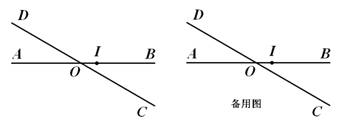
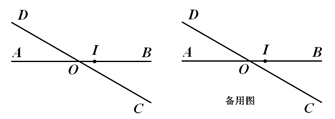
平面上两条直线AB、CD相交于点O，且∠BOD=150⁰（如图），现按如下要求规定此平面上点的“距离坐标”：

（1）点O的“距离坐标”为（0，0）；

（2）在直线CD上，且到直线AB的距离为p（p＞0）的点的“距离坐标”为（p，0）；在直线AB上，且到直线CD的距离为q（q＞0）的点的“距离坐标”为（0，q）；

（3）到直线AB、CD的距离分别为p、q（p＞0，q＞0）的点的“距离坐标”为（p，q）。

设M为此平面上的点，其“距离坐标”为（m，n），根据上述对点的“距离坐标”的规定，解决下列问题：

（1）画出图形（保留画图痕迹）：

①满足m=1且n=0的点的集合；

②满足m=n的点的集合；

（2）若点M在过点O且与直线CD垂直的直线l上，求m与n所满足的关系式。

（说明：图中OI长为一个单位长）

Answer 1

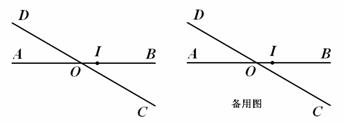
解：（1）①如图1中，F₁，F₂即为所求；

                 ②如图2中，两条角平分线即为所求。

            （2）如图3，过点M作MH⊥AB于点H。则

                 根据定义，MH=m，MO=n。

                 ∵∠BOD=150⁰，∠DOM=90⁰（∵l⊥CD），

                 ∴ ∠HOM=60⁰。

                 在Rt△MHO中，，

                 ∴ ，即，即。

                 ∴ m与n所满足的关系式为。