题目内容
在直角梯形ABCD中AD∥CB，∠A=90°，BD⊥CD，∠DBC=30°，DC=2，则AD= ．
【答案】分析：因为AD∥CB，∠DBC=30°，所以∠ADB=30°．在△BCD中运用三角函数可求BD，同理在△ABD中求AD．
解答：解：∵AD∥CB，∠DBC=30°，∴∠ADB=30°．
在Rt△BCD中，BD=
=
=2
．
在Rt△ADB中，AD=BD•cos30°=2
×
=3．
点评：此题主要利用了直角梯形中构成的直角三角形，运用三角函数知识计算求解．
解答：解：∵AD∥CB，∠DBC=30°，∴∠ADB=30°．
在Rt△BCD中，BD=
==2．在Rt△ADB中，AD=BD•cos30°=2
×=3．点评：此题主要利用了直角梯形中构成的直角三角形，运用三角函数知识计算求解．
练习册系列答案
灵星计算小达人系列答案
相关题目
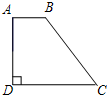如图，在直角梯形ABCD中，AB∥DC，∠D=90°，若AD=8，BC=10，则cosC的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
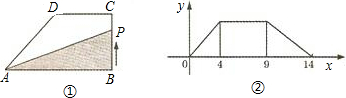
如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，且AB=BC=4AD，E是AB上的一点，DE⊥EC．求证：CE平分∠BCD．
如图，在直角梯形ABCD中，∠A=∠B=90°，∠C=45°，AB=4，AD=5，把梯形沿过点D的直线折叠，使点A刚好落在BC边上，则此时折痕的长为
如图，在直角梯形ABCD中，若AD=5，点A的坐标为（-2，7），则点D的坐标为（ ）