题目内容
如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连结AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.

(1)证明:连接AB ……1分
∵OP⊥BC
∴BO=CO ……2分
∴AB=AC
又∵AC=AD
∴AB=AD
∴∠ABD=∠ADB ……3分
又∵∠ABD=∠ACF
∴∠ACF=∠ADB ……4分
(2)解:过点A做AM⊥CF交CF的延长线于M,过点A做AN⊥BF于N,连接AF
则AN=m
∴∠ANB=∠AMC=90°
又∵∠ABN=∠ACM ,AB=AC
∴Rt⊿ABN≌Rt⊿ACM(AAS)
∴BN=CM ,AN=AM ……5分
又∵∠ANF=∠AMF=90°, AF公共
∴Rt⊿AFN≌Rt⊿AFM(HL)
∴NF=MF ……6分
∴BF+CF=BN+NF+CM-MF
=BN+CM=2BN=n ……7分
∴BN=![]()
∴CD=![]() ……8分
……8分
(3)过点D做DH⊥AO于N , 过点D做DQ⊥BC于Q ……9分
∵∠DAH+∠OAC=90°, ∠DAH+∠ADH=90°
∴∠OAC=∠ADH
又∵∠DHA=∠AOC=90°, AD=AC
∴Rt⊿DHA≌Rt⊿AOC(AAS)
∴DH=AO ,AH=OC ……10分
∴![]() =
=![]()
![]() =
=![]()


 53随堂测系列答案
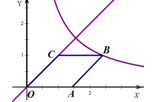
53随堂测系列答案 (2013•金华模拟)如图,点A在x轴的正半轴,菱形OABC的面积为
(2013•金华模拟)如图,点A在x轴的正半轴,菱形OABC的面积为 如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC.
如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,交连接AC、FC.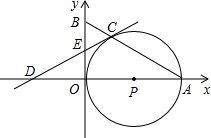 如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线
如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线 ,点B在双曲线
,点B在双曲线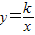 上,点C在直线y=x上,则k的值为 .
上,点C在直线y=x上,则k的值为 .
 ,点B在双曲线
,点B在双曲线 上,点C在直线y=x上,则k的值为____________.
上,点C在直线y=x上,则k的值为____________.