Question

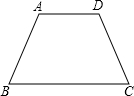
如图，在直角梯形ABCD中，BC∥AD，∠A=90°，AB=2，BC=3，AD=4，E为BC的中点，F为CD的中点，P为AD上一动点（不与A、D重合），由A向D运动，速度为1cm/s，设四边形PEFD的面积为y，当运动时间为x秒时，y与x的函数关系式是______．

Answer 1

过F作FH⊥BC于H，
则FH=

1

2

AB=1，
∵CB=3，E为BC的中点，
∴BE=CE=

3

2

，
∴y=S_t梯形ABCD-S_△EFC-S_梯形APEB，
=

1

2

×（3+4）×2-

1

2

×

3

2

×1-

1

2

•（x+

3

2

）•2，
=

19

4

-x．
故答案为：

19

4

-x．