题目内容
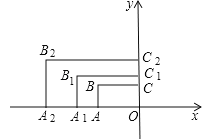
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
【答案】(﹣![]() ,
,![]() ).
).
【解析】
试题分析:∵在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,∵OA=2,OC=1.
倍,∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,∵OA=2,OC=1.
∵点B的坐标为(﹣2,1),∴点B1的坐标为(﹣2×![]() ,1×
,1×![]() ),∵将矩形A1OC1B1以原点O为位似中心放大
),∵将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2…,∴B2(﹣2×
倍,得到矩形A2OC2B2…,∴B2(﹣2×![]() ×
×![]() ,1×
,1×![]() ×
×![]() ),∴Bn(﹣2×
),∴Bn(﹣2×![]() ,1×
,1×![]() ),∵矩形AnOCnBn的对角线交点(﹣2×
),∵矩形AnOCnBn的对角线交点(﹣2×![]() ×
×![]() ,1×
,1×![]() ×
×![]() ),即(﹣
),即(﹣![]() ,
,![]() ),故答案为:(﹣
),故答案为:(﹣![]() ,
,![]() ).
).

练习册系列答案
相关题目