题目内容
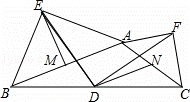
如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE的最小值为 ．
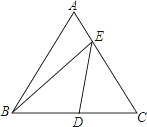
解：作B关于AC的对称点B′，连接BB′、B′D，交AC于E，此时BE+ED=B′E+ED=B′D，根据两点之间线段最短可知B′D就是BE+ED的最小值，
∵B、B′关于AC的对称，
∴AC、BB′互相垂直平分，
∴四边形ABCB′是平行四边形，
∵三角形ABC是边长为2，
∵D为BC的中点，
∴AD⊥BC，
∴AD=
，BD=CD=1，BB′=2AD=2，
作B′G⊥BC的延长线于G，
∴B′G=AD=，
在Rt△B′BG中，
BG=
=
=3，
∴DG=BG﹣BD=3﹣1=2，
在Rt△B′DG中，BD=
=
=．
故BE+ED的最小值为．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
CG2；③若AF=2DF，则BG=6GF；④CG与BD一定不垂直；⑤∠BGE的大小为定值．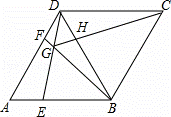
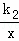的图象分别交于C、D两点，点D（2，﹣3），点B是线段AD的中点．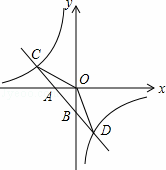
．
B．
C．
D．
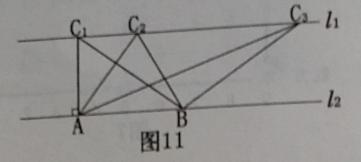
S四边形ABDN；③DE=DF；④DE⊥DF．其中正确的结论的个数是（ ）