题目内容
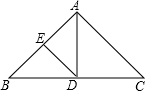 在△ABC中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.
在△ABC中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.求:(1)∠B的度数;(2)线段DE的长.
考点:等腰三角形的性质,直角三角形斜边上的中线
专题:
分析:(1)根据等腰三角形的两个底角相等和三角形的内角和定理就可求解;
(2)根据等腰三角形的三线合一的性质,得到AD是等腰△ABC底边BC上的高,然后根据直角三角形斜边上的中线等于斜边的一半即可求出DE的长.
(2)根据等腰三角形的三线合一的性质,得到AD是等腰△ABC底边BC上的高,然后根据直角三角形斜边上的中线等于斜边的一半即可求出DE的长.
解答:解:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠C=
(180°-∠A)=40°;
(2)∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,
∵点E是AB的中点,
∴DE=
AB=4.
∴∠B=∠C=
| 1 |
| 2 |
(2)∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,
∵点E是AB的中点,
∴DE=
| 1 |
| 2 |
点评:此题主要是运用了等腰三角形的性质,三角形的内角和定理和直角三角形斜边上的中线的性质,比较简单.

练习册系列答案
相关题目
计算(
-
+
)×12时,可以使运算简便的运算律是( )
| 4 |
| 3 |
| 1 |
| 6 |
| 3 |
| 2 |
| A、乘法交换律 |
| B、乘法结合律 |
| C、乘法分配律 |
| D、加法交换律和结合律 |
在下列各式中
①(-3)×4×2.3×(-5)
②3.5×(-20)×4.6×(-1)×(-6)×0
③(-1.5)×(-2.4)×(-3)×(-9)×5.3
④(-3)×(-4)×(-5)×(-7)×(-10)
以上的各式结果为负数的个数有( )
①(-3)×4×2.3×(-5)
②3.5×(-20)×4.6×(-1)×(-6)×0
③(-1.5)×(-2.4)×(-3)×(-9)×5.3
④(-3)×(-4)×(-5)×(-7)×(-10)
以上的各式结果为负数的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
汽车向东行驶3千米记作+3千米,那么汽车向西行驶5千米记作( )
| A、5千米 | B、-3千米 |
| C、0千米 | D、-5千米 |
在数轴上与原点距离3.5个单位长度的点所表示的有理数是( )
| A、3.5 | B、-3.5 |
| C、±3.5 | D、无法确定 |