题目内容
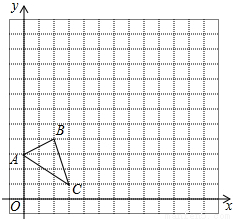
如图，
（1）在平面直角坐标系中作出△ABC以点O为位似中心，位似比为2的位似图形△A′B′C′；
（2）点B′的坐标是 （ ）；
（3）△A′B′C′的面积是 .
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
名校联盟快乐课堂系列答案黄冈创优卷系列答案题目内容
如图，
（1）在平面直角坐标系中作出△ABC以点O为位似中心，位似比为2的位似图形△A′B′C′；
（2）点B′的坐标是 （ ）；
（3）△A′B′C′的面积是 .
名校联盟快乐课堂系列答案黄冈创优卷系列答案
的中点，M是半径OD上任意一点．若∠BDC＝40°，则∠AMB的度数不可能是（ ）
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解答下列问题：
= ；
＜A＜
，∠A的正对值sadA的取值范围 ；
,其中∠A为锐角，试求sadA的值。
AC，DF=10，那么DE=_________________.
米，那么拦水坝斜坡的坡度和坡角分别为（ ）
B. 
C. 
D. 