题目内容
 在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为a(0°<a<90°),得到△A1B1C.如图,当AB∥CB1时,设A1B1与CB相交于点D.
在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为a(0°<a<90°),得到△A1B1C.如图,当AB∥CB1时,设A1B1与CB相交于点D.
(1)旋转角a为______度;
(2)证明:△A1CD是等边三角形.
(1)解:∵AB∥CB1,
∴∠B=∠BCB1=30°,
∴旋转角a为30度.
故答案为:30;
(2)证明:∵AB∥CB1,
∴∠B=∠BCB 1=30°,
∴∠A1CD=60°,
又∵∠A1=∠A=60°,
∴△A1CD是等边三角形.
分析:(1)根据AB∥CB1,得出∠B=∠BCB1=30°,即可求出旋转角a;
(2)根据∠B=∠BCB 1=30°,得出∠A1CD=60°,进而得出∠A1=∠A=60°即可求出△A1CD是等边三角形.
点评:此题主要考查了等边三角形的判定以及旋转的性质,根据平行线的性质得出∠B=∠BCB1=30°是解题关键.
∴∠B=∠BCB1=30°,
∴旋转角a为30度.
故答案为:30;
(2)证明:∵AB∥CB1,
∴∠B=∠BCB 1=30°,
∴∠A1CD=60°,
又∵∠A1=∠A=60°,
∴△A1CD是等边三角形.
分析:(1)根据AB∥CB1,得出∠B=∠BCB1=30°,即可求出旋转角a;
(2)根据∠B=∠BCB 1=30°,得出∠A1CD=60°,进而得出∠A1=∠A=60°即可求出△A1CD是等边三角形.
点评:此题主要考查了等边三角形的判定以及旋转的性质,根据平行线的性质得出∠B=∠BCB1=30°是解题关键.

练习册系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
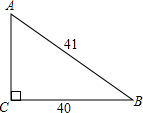 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=