题目内容
 已知:如图,在直角坐标系xOy中,Rt△OCD的一边OC在x轴上.∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
已知:如图,在直角坐标系xOy中,Rt△OCD的一边OC在x轴上.∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.(1)求该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.
分析:(1)根据线段的中点坐标的求法(线段中点的横纵坐标分别是线段2个端点的横纵坐标的和的一半)易得点A坐标,设出反比例函数的解析式,把A坐标代入即可;
(2)点B,D的横坐标相等,代入(1)中反比例函数的解析式中,求出点B的坐标,把A、B的坐标代入一次函数解析式,利用待定系数法求出函数解析式即可.
(2)点B,D的横坐标相等,代入(1)中反比例函数的解析式中,求出点B的坐标,把A、B的坐标代入一次函数解析式,利用待定系数法求出函数解析式即可.
解答: 解:(1)过点A作AE⊥x轴于点E.
解:(1)过点A作AE⊥x轴于点E.
∵∠OCD=90°,
∴AE∥CD.A为OD中点,OC=3,DC=4,
∴AE是△OCD的中位线,
∴OE=EC=
OC,
∴A(1.5,2);
设反比例函数解析式为y=
,
那么k=1.5×2=3,
∴y=
;
(2)当x=3时,y=1,
∴B(3,1);
设过A、B两点的直线的解析式为y=k2x+b,
则
,
解得:
.
∴y=-
x+3.
 解:(1)过点A作AE⊥x轴于点E.
解:(1)过点A作AE⊥x轴于点E.∵∠OCD=90°,
∴AE∥CD.A为OD中点,OC=3,DC=4,
∴AE是△OCD的中位线,
∴OE=EC=
| 1 |
| 2 |
∴A(1.5,2);
设反比例函数解析式为y=
| k |
| x |
那么k=1.5×2=3,
∴y=
| 3 |
| x |
(2)当x=3时,y=1,
∴B(3,1);
设过A、B两点的直线的解析式为y=k2x+b,
则
|
解得:
|
∴y=-
| 2 |
| 3 |
点评:本题考查用待定系数法求函数解析式,关键是求得相关点的坐标.要理解函数图象上点的坐标与函数解析式之间的关系和线段中点坐标的一般求算方法.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.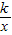 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
