题目内容
 在平面直角坐标系xOy中:已知抛物线
在平面直角坐标系xOy中:已知抛物线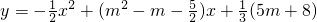 的对称轴为x=
的对称轴为x= ,设抛物线与y轴交于A点,与x轴交于B、C两点(B点在C点的左边),锐角△ABC的高BE交AO于点H.
,设抛物线与y轴交于A点,与x轴交于B、C两点(B点在C点的左边),锐角△ABC的高BE交AO于点H.
(1)求抛物线的解析式;
(2)在(1)中的抛物线上是否存在点P,使BP将△ABH的面积分成1:3两部分?如果存在,求出P点的坐标;如果不存在,请说明理由.
 解:(1)由题意:x=-
解:(1)由题意:x=-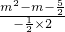 =-
=- ,
,化简,得:m2-m-2=0
解得:m1=-1,m2=2;
当m=-1时,函数解析式为:y=-
 x2-
x2- x+1(如右图),其中△ABC不符合锐角三角形的特点,故m=-1舍去;
x+1(如右图),其中△ABC不符合锐角三角形的特点,故m=-1舍去;当m=2时,函数解析式为:y=-
 x2-
x2- x+6;
x+6;综上,抛物线的解析式为:y=-
 x2-
x2- x+6.
x+6.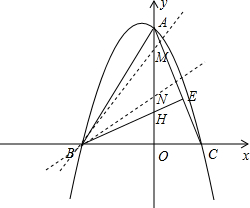 (2)由(1)知:抛物线的解析式为:y=-
(2)由(1)知:抛物线的解析式为:y=- x2-
x2- x+6(如右图);
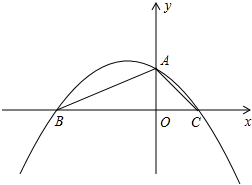
x+6(如右图);令x=0,则y=6,即 A(0,6);
令y=0,-
 x2-
x2- x+6=0,解得:x1=3,x2=-4;即 B(-4,0)、C(3,0);
x+6=0,解得:x1=3,x2=-4;即 B(-4,0)、C(3,0);∠OAC=∠HBO=90°-∠ACO,又∠AEH=∠BOH=90°,
∴Rt△BOH∽Rt△AOC,
∴
 =
=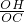 ,即
,即  =
=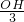 ,OH=2,AH=4;
,OH=2,AH=4;在线段AH上取AM=HN=
 AH=1,则 M(0,5)、N(0,3);
AH=1,则 M(0,5)、N(0,3);设直线BM的解析式为:y=kx+5,则有:-4k+5=0,k=
 ;
;∴直线BM:y=
 x+5.
x+5.同理,直线BN:y=
 x+3.
x+3.联立直线BM和抛物线y=-
 x2-
x2- x+6,有:
x+6,有: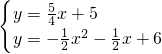 ,
,解得:
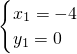 ,
,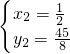
∴P1(
 ,
,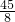 );
);同理,求直线BN与抛物线的交点P2(
 ,
,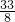 );
);综上,存在符合条件的P点,且坐标为:P1(
 ,
,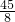 )、P2(
)、P2( ,
,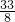 ).
).分析:(1)抛物线y=ax2+bx+c(a≠0)的对称轴方程为:x=-
 ,根据给出的抛物线对称轴列出关于m的方程,即可确定函数解析式,然后根据题干条件“锐角△ABC”对m值进行甄别.
,根据给出的抛物线对称轴列出关于m的方程,即可确定函数解析式,然后根据题干条件“锐角△ABC”对m值进行甄别.(2)首先根据题意画出对应图形,易发现△BHO∽△ACO,根据对应边成比例能求出OH、AH的长;在△ABH中,以AH为底进行讨论,若BP将△ABH分成1:3两部分,那么直线BP必将线段AH分成1:3两部分,首先求出直线BP的解析式,联立抛物线的解析式即可求出对应的P点坐标.
点评:此题考查了函数解析式的确定、函数图象交点坐标的解法、图形面积的求法等知识;(2)题中,能够将三角形的面积比转换为底边比是打开解题思路的关键所在.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为