题目内容
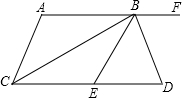
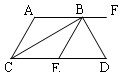
 如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为
如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据平行线的性质、角平分线的定义、余角的定义作答.
解答:①∵BC⊥BD,
∴∠DBE+∠CBE=90°,∠ABC+∠DBF=90°,
又∵BD平分∠EBF,
∴∠DBE=∠DBF,
∴∠ABC=∠CBE,
即BC平分∠ABE,正确;
②由AB∥CE,BC平分∠ABE、∠ACE易证∠ACB=∠CBE,∴AC∥BE正确;
③∵BC⊥AD,∴∠BCD+∠D=90°正确;
④无法证明∠DBF=60°,故错误.
故选C.
点评:此题难度中等,需灵活应用平行线的性质、角平分线的定义、余角的定义等知识点.
分析:根据平行线的性质、角平分线的定义、余角的定义作答.
解答:①∵BC⊥BD,
∴∠DBE+∠CBE=90°,∠ABC+∠DBF=90°,
又∵BD平分∠EBF,
∴∠DBE=∠DBF,
∴∠ABC=∠CBE,
即BC平分∠ABE,正确;
②由AB∥CE,BC平分∠ABE、∠ACE易证∠ACB=∠CBE,∴AC∥BE正确;
③∵BC⊥AD,∴∠BCD+∠D=90°正确;
④无法证明∠DBF=60°,故错误.
故选C.
点评:此题难度中等,需灵活应用平行线的性质、角平分线的定义、余角的定义等知识点.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
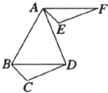 14、如图,AF∥BD,AE∥BC,且AF=BD,AE=BC,则线段EF是通过平移线段
14、如图,AF∥BD,AE∥BC,且AF=BD,AE=BC,则线段EF是通过平移线段 12、如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为( )
12、如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为( )