题目内容
【题目】已知![]() 与
与![]() 成正比例,且
成正比例,且![]() 时,
时,![]() .
.
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
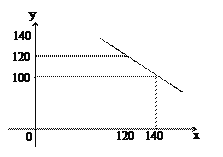
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当![]() 时,自变量
时,自变量![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】分析:(1)根据正比例的定义设y+4=kx(k≠0),然后把已知数据代入进行计算求出k值,即可得解;
(2)求出与坐标轴的交点,然后利用两点法作出函数图象即可;
(3)根据图象可得结论.
详解:(1)∵y+4与x成正比例,∴设y+4=kx(k≠0).
∵当x=6时,y=8,∴8+4=6k,解得:k=2,
∴y+4=2x,
∴函数关系式为:y=2x﹣4;
(2)当x=0时,y=﹣4,
当y=0时,2x﹣4=0,解得:x=2,
所以,函数图象经过点(0,﹣4),(2,0),
函数图象如图:

(3)由图象得:当﹣4≤y≤0时,自变量x的取值范围是:0≤x≤2.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目