Question

【题目】（数学问题）在同一直角坐标系内直线与，当满足什么条件时，这两条直线互相垂直？

探究问题：我们采取一般问题特殊化的策略来进行探究．

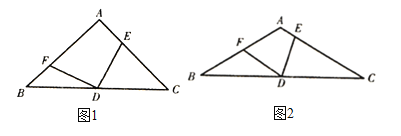
探究一：如图①，在同一直角坐标系内直线与有怎样的位置关系？

解：如图①，设点在直线上，则点一定在直线上．过点分别作的垂线，垂足分别为．

则，

∴

∵

∴

所以，在同一直角坐标系内直线与互相垂直．

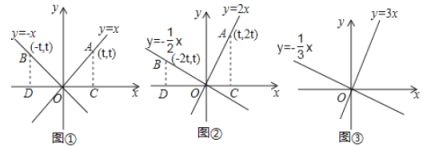
探究二：如图②，在同一直角坐标系内直线上，则点一定在直线上．过点分别作轴的垂线，垂足分别为．

∵，，，

∴，

又∵

∴

∴

又∵

∴

∵

∴

所以，在同一直角坐标系内直线与互相垂直．

探究三：如图③，在同一直角坐标系内直线与有怎样的位置关系？

（仿照上述方法解答，写出探究过程）

（1）在同一直角坐标系内直线与，当满足数量关系为 时，这两条直线互相垂直．

（2）在同一直角坐标系内已知直线与直线，使它与直线互相垂直，的值为： ；两直线垂足的坐标为： ．

Answer 1

【答案】探究三：互相垂直，详见解析；（1）；（2）k= -5，（2，0.4）

【解析】

探究三：仿照探究一与探究二，在两直线与上取点，证明三角形全等，由此得到结论；

（1）由探究即可得到答案；

（2）利用前面的结论得到k的值，再解两直线解析式组成的方程组即可得到答案.

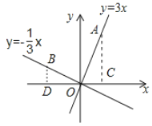
探究三：在同一直角坐标系内直线与互相垂直，

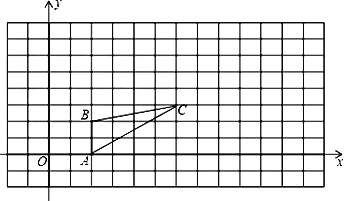
如图，设点A(a，3a)在直线y=3x上，则点B（-3a，a）在直线上，

作AC⊥x轴，BD⊥x轴，

∵OC=a，AC=3a，OD=3a，BD=a，

∴，，

又∵，

∴△AOC≌△OBD，

∴，

又∵，

∴，

∵，

∴

∴在同一直角坐标系内直线与互相垂直

（1）由探究一、二、三可知，当两条直线在同一平面内互相垂直时，两条直线的k值互为负倒数，

∴在同一直角坐标系内直线与，当这两条直线互相垂直时，，

故答案为：；

（2）∵直线与直线互相垂直，

∴0.2k=-1，

∴k=-5，

∴该直线的解析式为y=-5x+10.4，

解方程组，得，

∴两直线垂足的坐标为（2,0.4），

故答案为：k=-5，（2，0.4）.