��Ŀ����
����ABCD�У�AD��BC��BC=20cm��AD=10cm��������������P��Q�ֱ��B��D����ͬʱ��������P��ÿ��2cm���ٶ���BC���յ�C�ƶ�����Q��ÿ��1cm���ٶ���DA���յ�A�ƶ����߶�PQ��BD�ཻ�ڵ�E����E��EF��BC��CD�ڵ�F������QF��BC���ӳ����ڵ�H���趯��P��Q�ƶ���ʱ��Ϊt����λ���룬0��t��10������1����tΪ��ֵʱ���ı���PCDQΪƽ���ı��Σ�
��2����P��Q�ƶ��Ĺ����У��߶�PH�ij��Ƿ����ı䣿������䣬����߶�PH�ij�������ı䣬��˵�����ɣ�

���⣺��1����AD��BC��BC=20cm��AD=10cm����P��Q�ֱ��B��D����ͬʱ��������P��ÿ��2cm���ٶ���BC���յ�C�ƶ�����Q��ÿ��1cm���ٶ���DA���յ�A�ƶ���
��DQ=t��PC=20��2t��
�����ı���PCDQΪƽ���ı��Σ���DQ=PC��
��20��2t=t��
��ã�t= ��
��
��2���߶�PH�ij����䣬
��AD��BH��P��Q������ٶȱ�Ϊ2��1��
��QD��BP=1��2��
��QE��EP=ED��BE=1��2��
��EF��BH��
��ED��DB=EF��BC=1��3��
��BC=20��
��EF= ��
��
�� ��
�� =
= ��
��
��PH=20cm������:
����1������ı���PCDQΪƽ���ı��Σ���DQ=CP������P��Q������˶��ٶȣ�����˶�ʱ��t�����DQ��CP�ij��ȱ���ʽ���ⷽ�̼��ɣ�
��2��PH�ij��Ȳ��䣬����P��Q������ٶȱȣ������Ƴ�QD��BP=1��2������ƽ���ߵ������Ƴ����������ƣ��ó����Ʊȣ������Ƴ�PH=20��
��DQ=t��PC=20��2t��
�����ı���PCDQΪƽ���ı��Σ���DQ=PC��
��20��2t=t��
��ã�t=
 ��
����2���߶�PH�ij����䣬
��AD��BH��P��Q������ٶȱ�Ϊ2��1��
��QD��BP=1��2��
��QE��EP=ED��BE=1��2��
��EF��BH��
��ED��DB=EF��BC=1��3��
��BC=20��
��EF=
 ��
����
 ��
�� =
= ��
����PH=20cm������:
����1������ı���PCDQΪƽ���ı��Σ���DQ=CP������P��Q������˶��ٶȣ�����˶�ʱ��t�����DQ��CP�ij��ȱ���ʽ���ⷽ�̼��ɣ�
��2��PH�ij��Ȳ��䣬����P��Q������ٶȱȣ������Ƴ�QD��BP=1��2������ƽ���ߵ������Ƴ����������ƣ��ó����Ʊȣ������Ƴ�PH=20��

��ϰ��ϵ�д�
 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
�����Ŀ
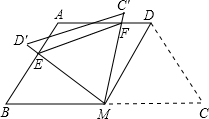 ��ͼ����������ABCD�У�AD��BC��AD=AB=CD=2����C=60�㣬M��BC���е㣮
��ͼ����������ABCD�У�AD��BC��AD=AB=CD=2����C=60�㣬M��BC���е㣮 DE��
DE�� ��ͼ��������ABCD�У�AD��BC��AB=CD����E��BC���ӳ����ϣ��ҡ�BDE=��ADC����֤��AB•BD=DE•AD��
��ͼ��������ABCD�У�AD��BC��AB=CD����E��BC���ӳ����ϣ��ҡ�BDE=��ADC����֤��AB•BD=DE•AD��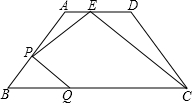 ��ͼ���ڵ�������ABCD�У�AD��BC��AB=5��AD=6��BC=12����E��AD���ϣ���AE��ED=1��2����P��AB���ϵ�һ�����㣬��P����A��B�غϣ�����P��PQ��CE��BC�ڵ�Q����AP=x��CQ=y����y��x֮��ĺ�����ϵ��
��ͼ���ڵ�������ABCD�У�AD��BC��AB=5��AD=6��BC=12����E��AD���ϣ���AE��ED=1��2����P��AB���ϵ�һ�����㣬��P����A��B�غϣ�����P��PQ��CE��BC�ڵ�Q����AP=x��CQ=y����y��x֮��ĺ�����ϵ�� �ֱ�CD��BC�ڵ�F��E����AD=3��BC=12��
�ֱ�CD��BC�ڵ�F��E����AD=3��BC=12��