题目内容

在平面直角坐标中，边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点，现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线

上时停止旋转．旋转过程中，AB边交直线

于点M，BC边交x轴于点N（如图1）
（1）求边AB在旋转过程中所扫过的面积；
（2）设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论；
（3）设MN=

，当

为何值时△OMN的面积最小，最小值是多少？并直接写出此时△BMN内切圆的半径。

解：（1）如图，

=

（2）p值无变化
证明：延长BA交y轴于E点，
在

中，

所以，

≌

所以，OE=ON，AE=CN
在

中

所以，

≌

所以，MN==ME=AM+AE=AM+CN
所以，P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2
（3）设

，
因为，

≌

，
所以，

在

中，

所以，

所以，

所以，当

时，

的面积最小

的内切圆半径为

练习册系列答案

名师选优冲刺卷系列答案

全程优选卷系列答案

99加1活页卷系列答案

世纪百通单元综合大考卷系列答案

鸿图图书名师100分系列答案

名题金卷系列答案

奇迹试卷系列答案

经纶学典小学全程卷系列答案

名师点拨培优密卷系列答案

通城学典小题精练系列答案

相关题目

27、如图（1），在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．容易证得：CE=CF；
（1）在图1中，若G在AD上，且∠GCE=45°．试猜想GE、BE、GD三线段之间的数量关系，并证明你的结论．
（2）运用（1）中解答所积累的经验和知识，完成下面两题：
①如图（2），在四边形ABCD中∠B=∠D=90°，BC=CD，点E，点G分别是AB边，AD边上的动点．若∠BCD=α°，∠ECG=β°，试探索当α和β满足什么关系时，图（1）中GE、BE、GD三线段之间的关系仍然成立，并说明理由．
②在平面直角坐标中，边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图（3））．设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论．

在平面直角坐标中，边长为2的正三角形OAB的顶点A在y轴正半轴上，点O在原点．现将正三角形OAB绕O点顺时针旋转，当A点第一次落在直线y=

x上时停止旋转，旋转过程中，AB边交直线y=

x于点M，点B在x轴投影为N（如图）．求：
（1）初始状态时直线AB的解析式；
（2）OA边在旋转过程中所扫过的面积；
（3）△OMN从开始运动到到停止状态前后面积比．

在平面直角坐标中，边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转．旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图1）．
（1）求边AB在旋转过程中所扫过的面积；
（2）设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论；
（3）设MN=m，当m为何值时△OMN的面积最小，最小值是多少？并直接写出此时△BMN内切圆的半径．

在平面直角坐标中，边长为2的正三角形OAB的顶点A在y轴正半轴上，点O在原点．现将正三角形OAB绕O点顺时针旋转，当A点第一次落在直线 $数学公式$ 上时停止旋转，旋转过程中，AB边交直线 $数学公式$ 于点M，点B在x轴投影为N（如图）．求：
（1）初始状态时直线AB的解析式；
（2）OA边在旋转过程中所扫过的面积；
（3）△OMN从开始运动到到停止状态前后面积比．

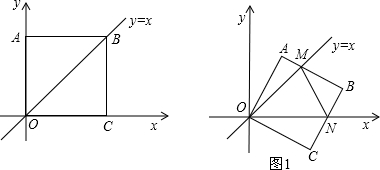
在平面直角坐标中，边长为2的正三角形OAB的顶点A在y轴正半轴上，点O在原点．现将正三角形OAB绕O点顺时针旋转，当A点第一次落在直线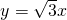

上时停止旋转，旋转过程中，AB边交直线

于点M，点B在x轴投影为N（如图）．求：
（1）初始状态时直线AB的解析式；
（2）OA边在旋转过程中所扫过的面积；
（3）△OMN从开始运动到到停止状态前后面积比．