题目内容
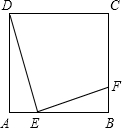 如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.(1)求证:△ADE∽△BEF;
(2)设正方形的边长为4,AE=x,BF=y;求y关于x的函数解析式及函数的定义域;
(3)当x取什么值时,y有最大值?求出这个最大值.并指出该函数图象的变化情况.
分析:(1)根据正方形的性质及余角的性质得出△ADE与△BEF的两对应角相等,从而得出△ADE∽△BEF;
(2)根据相似三角形的性质得出y关于x的函数解析式及函数的定义域;
(3)当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值.
(2)根据相似三角形的性质得出y关于x的函数解析式及函数的定义域;
(3)当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值.
解答:(1)证明:∵ABCD是正方形,∴∠DAE=∠EBF=90°,(1分)
∴∠ADE+∠AED=90°,
又EF⊥DE,∴∠AED+∠BEF=90°,(1分)
∴∠ADE=∠BEF,(1分)
∴△ADE∽△BEF(1分)
(2)解:由(1)△ADE∽△BEF,AD=4,BE=4-x
得:
=
,即:
=
,(1分)
得:y=-
x2+x=-
(x2-4x)=-
(x-2)2+1,(0<x<4)(2分)
(3)解:当x=2时,y有最大值,y的最大值为1.(1分)
该函数图象在对称轴x=2的左侧部分是上升的,右侧部分是下降的.(2分)
∴∠ADE+∠AED=90°,
又EF⊥DE,∴∠AED+∠BEF=90°,(1分)
∴∠ADE=∠BEF,(1分)
∴△ADE∽△BEF(1分)
(2)解:由(1)△ADE∽△BEF,AD=4,BE=4-x
得:
| BF |
| AE |
| BE |
| AD |
| y |
| x |
| 4-x |
| 4 |
得:y=-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(3)解:当x=2时,y有最大值,y的最大值为1.(1分)
该函数图象在对称轴x=2的左侧部分是上升的,右侧部分是下降的.(2分)
点评:本题考查了相似三角形的判定和性质以及二次函数的综合应用.确定个二次函数的最值是,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 23、如图所示,E是正方形ABCD的边CD上一点,将△AED绕点A顺时针旋转90°,得到△AFB,则AE与AF有何关系?试说明理由.
23、如图所示,E是正方形ABCD的边CD上一点,将△AED绕点A顺时针旋转90°,得到△AFB,则AE与AF有何关系?试说明理由. 18、如图所示,ABCD是正方形,BE⊥BF,BE=BF,试判断AE与FC的位置关系,并给出证明.
18、如图所示,ABCD是正方形,BE⊥BF,BE=BF,试判断AE与FC的位置关系,并给出证明. 如图所示,E是正方形ABCD的边BC延长线上的点,且BC=CE.
如图所示,E是正方形ABCD的边BC延长线上的点,且BC=CE.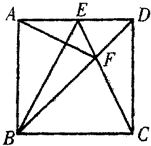 23、如图所示,E是正方形ABCD中AD边上的中点,BD与CE交于点F.请你根据图形判断AF与BE的位置具有什么关系?并给予证明.
23、如图所示,E是正方形ABCD中AD边上的中点,BD与CE交于点F.请你根据图形判断AF与BE的位置具有什么关系?并给予证明. 如图所示,P是正方形ABCD的边CD上一点,∠BAP的角平分线交BC于Q,
如图所示,P是正方形ABCD的边CD上一点,∠BAP的角平分线交BC于Q,