题目内容
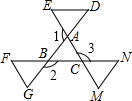
 如图所示,求∠D+∠E+∠F+∠G+∠M+∠N=________.
如图所示,求∠D+∠E+∠F+∠G+∠M+∠N=________.
360°
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠D+∠E=∠1,∠F+∠G=∠2,∠M+∠N=∠3,再根据三角形的外角和等于360°解答.
解答:如图,由三角形的外角性质得,∠D+∠E=∠1,∠F+∠G=∠2,∠M+∠N=∠3,
∵△ABC的外角和等于360°,
即∠1+∠2+∠3=360°,
∴∠D+∠E+∠F+∠G+∠M+∠N=360°.
故答案为:360°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及多边形的外角和等于360°,熟记性质是解题的关键.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠D+∠E=∠1,∠F+∠G=∠2,∠M+∠N=∠3,再根据三角形的外角和等于360°解答.
解答:如图,由三角形的外角性质得,∠D+∠E=∠1,∠F+∠G=∠2,∠M+∠N=∠3,
∵△ABC的外角和等于360°,
即∠1+∠2+∠3=360°,
∴∠D+∠E+∠F+∠G+∠M+∠N=360°.
故答案为:360°.

点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及多边形的外角和等于360°,熟记性质是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
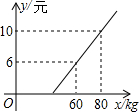 票,行李票费用y(元)是行李质量x(kg)的一次函数,其图象如图所示,求:
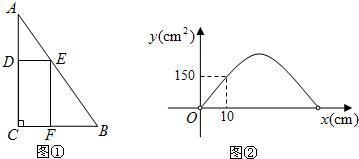
票,行李票费用y(元)是行李质量x(kg)的一次函数,其图象如图所示,求: 19、一株荷叶高出水面1m,一阵风吹来,荷叶被吹得贴着水面,这时它偏离原来的位置有3米远,如图所示,求荷叶的高度和水面的深度.
19、一株荷叶高出水面1m,一阵风吹来,荷叶被吹得贴着水面,这时它偏离原来的位置有3米远,如图所示,求荷叶的高度和水面的深度. 如图,是某个几何体的三视图,
如图,是某个几何体的三视图, 正比例函数y=kx的图象经过点P,如图所示,求这个正比例函数的解析式.
正比例函数y=kx的图象经过点P,如图所示,求这个正比例函数的解析式.