题目内容
【题目】已知:如图数轴上两点A、B所对应的数分别为-3、1,点P在数轴上从点A出发以每秒钟2个单位长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(2)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度;
(3)在(2)的条件下,当点P和点Q刚好相距1个单位长度时,数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小,若存在,直接写出点C所对应的数,若不存在,试说明理由.

【答案】(1)![]() ;(2)P出发
;(2)P出发![]() 秒或
秒或![]() 秒;(3)见解析.
秒;(3)见解析.
【解析】
(1)由题意可知运动t秒时P点表示的数为-3+2t,Q点表示的数为1-t,若P、Q相遇,则P、Q两点表示的数相等,由此可得关于t的方程,解方程即可求得答案;
(2)由点P比点Q迟1秒钟出发,则点Q运动了(t+1)秒,分相遇前相距1个单位长度与相遇后相距1个单位长度两种情况分别求解即可得;
(3)设点C表示的数为a,根据两点间的距离进行求解即可得.
(1)由题意可知运动t秒时P点表示的数为-5+t,Q点表示的数为10-2t;
若P,Q两点相遇,则有
-3+2t=1-t,
解得:t=![]() ,
,
∴![]() ,
,
∴点P和点Q相遇时的位置所对应的数为![]() ;
;
(2)∵点P比点Q迟1秒钟出发,∴点Q运动了(t+1)秒,
若点P和点Q在相遇前相距1个单位长度,
则![]() ,
,
解得:![]() ;
;
若点P和点Q在相遇后相距1个单位长度,
则2t+1×(t+1) =4+1,
解得:![]() ,
,
综合上述,当P出发![]() 秒或
秒或![]() 秒时,P和点Q相距1个单位长度;
秒时,P和点Q相距1个单位长度;
(3)①若点P和点Q在相遇前相距1个单位长度,
此时点P表示的数为-3+2×![]() =-
=-![]() ,Q点表示的数为1-(1+
,Q点表示的数为1-(1+![]() )=-
)=-![]() ,
,
设此时数轴上存在-个点C,点C表示的数为a,由题意得
AC+PC+QC=|a+3|+|a+![]() |+|a+
|+|a+![]() |,
|,
要使|a+3|+|a+![]() |+|a+
|+|a+![]() |最小,
|最小,
当点C与P重合时,即a=-![]() 时,点C到点A、点P和点Q这三点的距离和最小;
时,点C到点A、点P和点Q这三点的距离和最小;
②若点P和点Q在相遇后相距1个单位长度,
此时点P表示的数为-3+2×![]() =-
=-![]() ,Q点表示的数为1-(1+
,Q点表示的数为1-(1+![]() )=-
)=-![]() ,
,
此时满足条件的点C即为Q点,所表示的数为![]() ,
,
综上所述,点C所表示的数分别为-![]() 和-
和-![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表: 甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图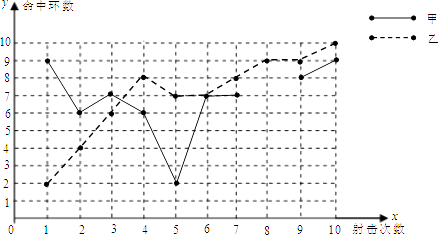
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?