题目内容
图1的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图.若图2中,∠AED=15°,则∠BCE的度数为何?( )

|
| A. | 30 | B. | 32.5 | C. | 35 | D. | 37.5 |
考点:
翻折变换(折叠问题)。
分析:
由题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,即可得△ABE、△A′BE皆为30°、60°、90° 的三角形,然后可求得∠AED′的度数,又由∠AED=15°,即可求得∠DED′的度数,继而求得∠BCE=∠2的度数.
解答:
解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
∴△ABE、△A′BE皆为30°、60°、90° 的三角形,
∴∠1=∠AEB=60°,
∴∠AED′=180°﹣∠1﹣∠AEB=180°﹣60°﹣60°=60°,
∴∠DED′=∠AED+∠AED′=15°+60°=75°,
∴∠2=![]() ∠DED′=37.5°,
∠DED′=37.5°,
∵A′D′∥BC,
∴∠BCE=∠2=37.5°.
故选D.

点评:
此题考查了折叠的性质、矩形的性质以及含30°角的直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系.

练习册系列答案
相关题目
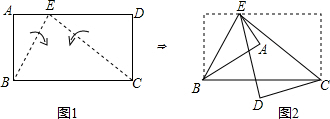
 图1的长方形ABCD中,E点在AD上,且BE=2AE.分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图.若图2中,∠AED=15°,则∠BCE的度数为何?________.
图1的长方形ABCD中,E点在AD上,且BE=2AE.分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图.若图2中,∠AED=15°,则∠BCE的度数为何?________.