题目内容
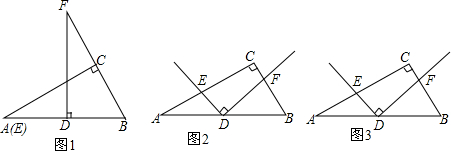
20.在Rt△ABC中,∠ACB=90°,∠A=30°,D为AB的中点,点E在线段AC上,点F在直线BC上,∠EDF=90°.(1)如图1,若点E与点A重合,点F在BC的延长线上,则此时$\frac{DE}{DF}$=$\frac{\sqrt{3}}{3}$;
(2)若点E在线段AC上运动,点F在线段BC上随之运动(如图2),请猜想在此过程中$\frac{DE}{DF}$的值是否发生改变.若不变,请求出$\frac{DE}{DF}$的值;若改变,请说明理由.
(3)在(2)的条件下,在线段EC上取一点G,在线段CB的延长线上取一点H,其中$\frac{EG}{FH}=k$,请问k为何值时,恒有∠GDH=90°.请在图3中补全图形,直接写出符合题意的k值,并以此为条件,证明∠GDH=90°.
分析 (1)根据直角三角形的性质和三角形全等的判定定理证明△ACB≌△FDB,得到∠F=∠A=30°,根据正切的概念解答;
(2)过点D作DM⊥AB交BC的延长线于点M,证明△ADE∽△MDF,得到$\frac{DE}{DF}=\frac{DA}{DM}$,计算即可;
(3)根据题意画出图形,根据相似三角形的判定定理证明△EGD∽△FHD即可.
解答 解:(1)$\frac{DE}{DF}$=$\frac{{\sqrt{3}}}{3}$,
∵∠ACB=90°,∠A=30°,
∴BC=$\frac{1}{2}$AB,
∵D为AB的中点,
∴BD=$\frac{1}{2}$AB,
∴BD=BC,
在△ACB和△FDB中,
$\left\{\begin{array}{l}{∠ACB=∠FDB}\\{BC=BD}\\{∠B=∠B}\end{array}\right.$,
∴△ACB≌△FDB,
∴∠F=∠A=30°,
∴$\frac{DE}{DF}$=$\frac{BD}{DF}$=tan30°=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$;
(2)猜想:在此过程中,$\frac{DE}{DF}$的值不变,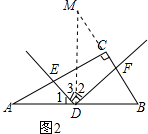
如图2,过点D作DM⊥AB交BC的延长线于点M.
∴∠MDA=∠MDB=90°,即∠1+∠3=90°
又∵∠EDF=∠2+∠3=90°
∴∠1=∠2
∵∠ACB=∠MDB=90°
∴∠A=90°-∠B,∠M=90°-∠B
∴∠A=∠M
∴△ADE∽△MDF,
∴$\frac{DE}{DF}=\frac{DA}{DM}$,
∵D为AB中点,
∴DA=DB,
∴$\frac{DA}{DM}=\frac{DB}{DM}=tanM=tan{30^o}=\frac{{\sqrt{3}}}{3}$
∴在此过程中,$\frac{DE}{DF}$的值不变,恒为$\frac{{\sqrt{3}}}{3}$;
(3)k=$\frac{{\sqrt{3}}}{3}$,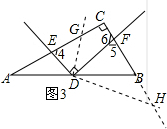
证明:由(2)得$\frac{DE}{DF}=\frac{{\sqrt{3}}}{3}=k=\frac{EG}{FH}$
∵四边形CEDF中,∠ACB=∠EDF=90°,
∴∠4+∠6=360°-∠ACB-∠EDF=180°
又∵∠5+∠6=180°
∴∠4=∠5
∴△EGD∽△FHD,
∴∠EDG=∠FDH
∵∠EDF=∠EDG+∠FDG=90°
∴∠FDH+∠FDG=90°
即∠GDH=90°.
点评 本题考查的是直角三角形的性质、相似三角形的判定和性质、全等三角形的判定和性质,以及锐角三角函数的概念,正确作出辅助线、灵活运用定理是解题的关键.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案| A. | 1-(x-3)=1 | B. | 3-2(x-3)=6 | C. | 2-3(x-3)=6 | D. | 3-2(x-3)=1 |
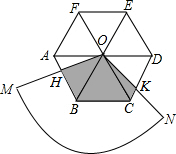 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.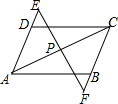 如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.
如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.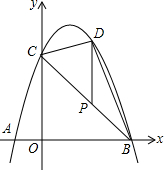 如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).
如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).