题目内容
已知函数y=y1+y2,y1与x+1成正比例,y2与x2成反比例,且x=1时y=4,x=-1时y=2,求:
(1)y关于x的函数关系式;
(2)当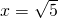 时y的值.
时y的值.
解:(1)∵y1与x+1成正比例,y2与x2成反比例,
∴可设y1=k1(x+1),y2= ,
,
∴y=y1+y2=k1(x+1)+ ,
,
∵当x=1时y=4,x=-1时y=2,
∴2k1+k2=4,k2=2,
解得k1=1,k2=2,
∴y关于x的函数关系式为:y=x+ +1,
+1,
(2)当x= 时有,y=
时有,y= +
+ +1=
+1= +
+ .
.
分析:(1)由题意,y1与x+1成正比例,可设y1=k1(x+1),y2与x2成反比例,可设y2= ,代入函数y=y1+y2,得到y与x的解析式,再根据当x=1时y=4,x=-1时y=2,求出看,k1,k2,从而求出)y关于x的函数关系式;
,代入函数y=y1+y2,得到y与x的解析式,再根据当x=1时y=4,x=-1时y=2,求出看,k1,k2,从而求出)y关于x的函数关系式;
(2)把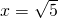 代入(1)求得的解析式,从而求出y值.
代入(1)求得的解析式,从而求出y值.
点评:此题主要考查正比例函数和反比例函数的定义和性质,还考查用待定系数法求函数的解析式,看似复杂,其实比较简单.
∴可设y1=k1(x+1),y2=
 ,
,∴y=y1+y2=k1(x+1)+
 ,
,∵当x=1时y=4,x=-1时y=2,
∴2k1+k2=4,k2=2,
解得k1=1,k2=2,
∴y关于x的函数关系式为:y=x+
 +1,
+1,(2)当x=
 时有,y=
时有,y= +
+ +1=
+1= +
+ .
.分析:(1)由题意,y1与x+1成正比例,可设y1=k1(x+1),y2与x2成反比例,可设y2=
 ,代入函数y=y1+y2,得到y与x的解析式,再根据当x=1时y=4,x=-1时y=2,求出看,k1,k2,从而求出)y关于x的函数关系式;
,代入函数y=y1+y2,得到y与x的解析式,再根据当x=1时y=4,x=-1时y=2,求出看,k1,k2,从而求出)y关于x的函数关系式;(2)把
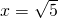 代入(1)求得的解析式,从而求出y值.
代入(1)求得的解析式,从而求出y值.点评:此题主要考查正比例函数和反比例函数的定义和性质,还考查用待定系数法求函数的解析式,看似复杂,其实比较简单.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目