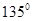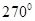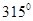题目内容

如图，一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是_____________.
10

试题分析：将长方体纸箱按照不同方式展开，分别根据勾股定理求出不同展开图中AB的长，再找到其中最短者即为蚂蚁所行的最短路程．如图（1）所示：AB=如图（2）所示：AB=由于所以最短路径为10．

点评：本题考查了平面展开---最短路径问题，解题的关键是将长方体展开，构造直角三角形，然后利用勾股定理解答
练习册系列答案
相关题目
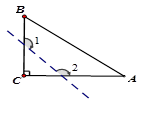
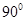如图，已知△ABC为直角三角形，∠C=，若沿图中虚线剪去∠C，则 ∠1+∠2等于 (      )
A．B．C．D．
如下图，在△ABC中，AD⊥BC于D，若AB2=BD·BC，
求证：△ABC是直角三角形。
阅读下面材料：
问题：如图①，在△ABC中， D是BC边上的一点，若∠BAD=∠C=2∠DAC=45°，DC=2．求BD的长．
小明同学的解题思路是：利用轴对称，把△ADC进行翻折，再经过推理、计算使问题得到解决．
（1）请你回答：图中BD的长为   ；
（2）参考小明的思路，探究并解答问题：如图②，在△ABC中，D是BC边上的一点，若∠BAD=∠C=2∠DAC=30°，DC=2，求BD和AB的长．
            
图①                                   图②
一个多边形的内角和是外角和的3倍，则这个多边形的边数为         .
如图，AD是ΔABC的外角∠CAE的平分线，∠B=30°，∠DAE=55°，试求：(1)∠BAC的度数；  (2)∠ACB的度数 
  
如图，在△ABC中，AB=AC，

（1）若P是BC边上的中点，连结AP，求证：BP×CP=AB2一AP2；
（2）若P是BC边上任意一点，上面的结论还成立吗?若成立，请证明，若不成立，请说明理由；
（3）若P是BC边延长线上一点，线段AB、AP、BP、CP之间有什么样的关系?请证明你的结论？
如图，△ABC中，∠A=90º，∠ABC与∠ACB的角平分线交于点I，△ABC的外角∠DBC与∠BCE的角平分线交于P.

（1）则∠BIC=       ，∠P=       （直接写出答案）；
（2）若∠A的度数为xº时，求∠BIC，∠P的度数.
如图所示，∠1=∠2，AE⊥OB于E，BD⊥OA于D，交点为C，则图中全等三角形共有（　　）
A．2对B．3对C．4对D．5对

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网